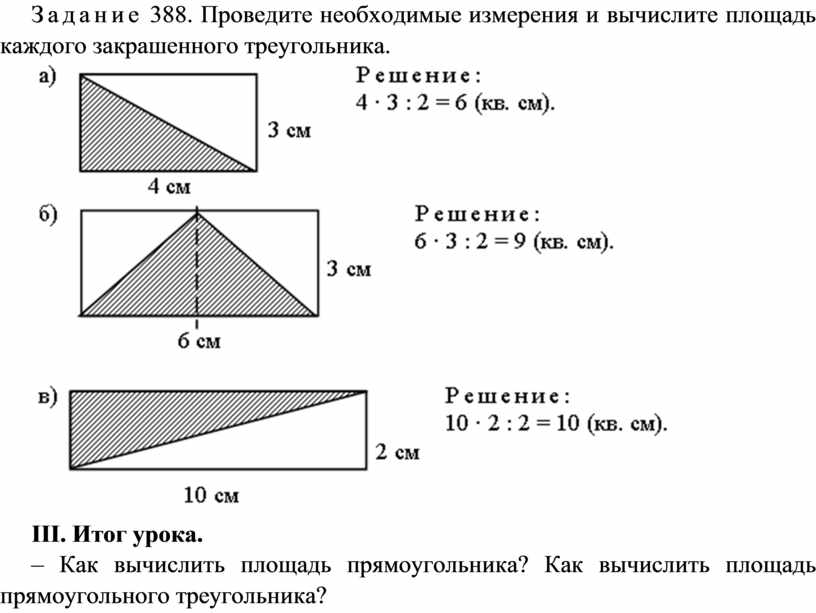
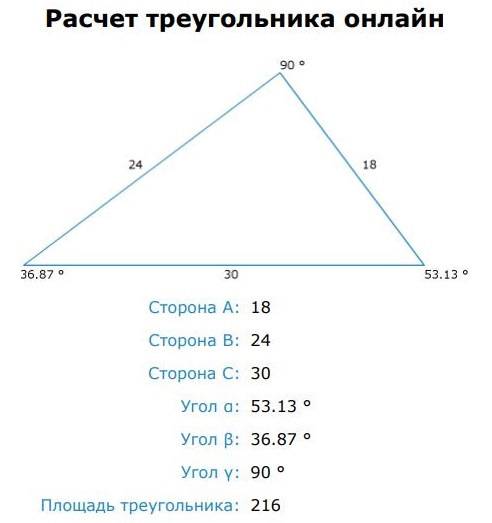
???? Когда нужно знать площадь треугольника?
Знание площади треугольника может быть полезно во многих сферах жизни, включая математику, науки, строительство, дизайн и другие области.
Вот некоторые конкретные примеры, когда необходимо знать площадь треугольника:
- В математике – для решения задач на нахождение площади треугольника или расчета других параметров на основе площади.
- В науках – для расчета площади треугольной формы в различных контекстах, например, при изучении геометрии или физики.
- В строительстве – для расчета площади треугольного участка поверхности, например, для закупки материалов или расчета стоимости работ.
- В дизайне – для расчета площади треугольных участков земли или других поверхностей, например, для планировки ландшафта или выбора размера ковра.
- В повседневной жизни – для решения различных задач, например, для расчета площади треугольной поверхности мебели или для оценки площади треугольного участка земли в саду.
Знание площади треугольника может быть полезным во многих ситуациях, где треугольная форма играет важную роль, и поможет справиться с различными задачами более эффективно.
Как посчитать площадь комнаты в квадратных метрах
Основные этапы работ
Расчёт площади крыши всегда следует начинать с :
- ознакомления с будущим проектом кровли дома и запоминания наиболее ключевых параметров: длины конька, угла уклона, высоты, ширины и длины;
- определения типа кровельного материала, который будет использоваться.
Одной из самых важных характеристик является специальный расчетный коэффициент, присутствующий абсолютно во всех формулах. Его значение зависит от угла ската крыши и определяется следующими соотношениями :
- при наклоне скатов 9°, коэффициент составит 1,01;
- для 14° – 1,03;
- для 18° – 1, 05;
- при 23° – 1,08;
- при 27° – 1,12;
- для 34° – 1,2.
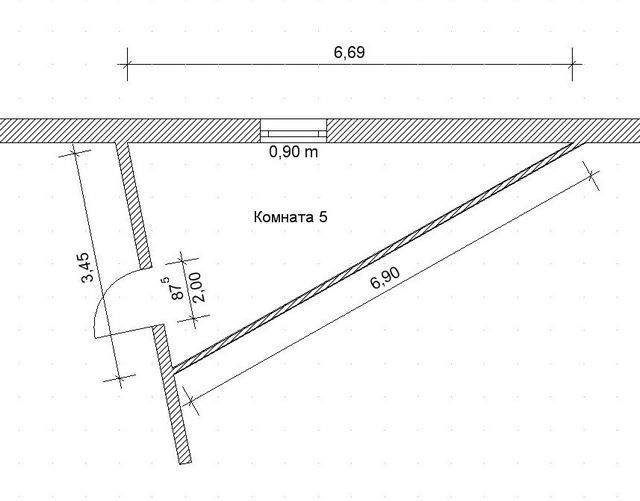
Расчет площади пола в комнате неправильной формы
У комнат, имеющих неправильную форму, рассчитать площадь намного сложнее. Сложности добавляют такие элементы, как арки, ниши в форме полукруга, скошенные стены и т. д. По сути, принцип расчета тот же – нужно разбить помещение на несколько ровных фигур и высчитать площадь каждой отдельно, а потом суммировать. Но площадь круга или треугольника считается уже по другим формулам.
Пол неправильной формы
Например, площадь треугольника высчитывается так: длина основания умножается на высоту треугольника и делится на 2.
Расчет площади комнаты неправильной формы
На заметку! Проще всего по возможность делить все помещение на ровные фигуры типа квадратов и треугольников и считать их площади отдельно, а потом суммировать.
Площадь многоуровневых полос посчитать не так сложно, как кажется. Просто считаются площади отдельных сегментов и суммируются. Если ступени необходимо отделать таким же напольным материалом, как и остальной пол, то достаточно измерить площадь боковой части каждой ступени и приплюсовать к общей цифре.
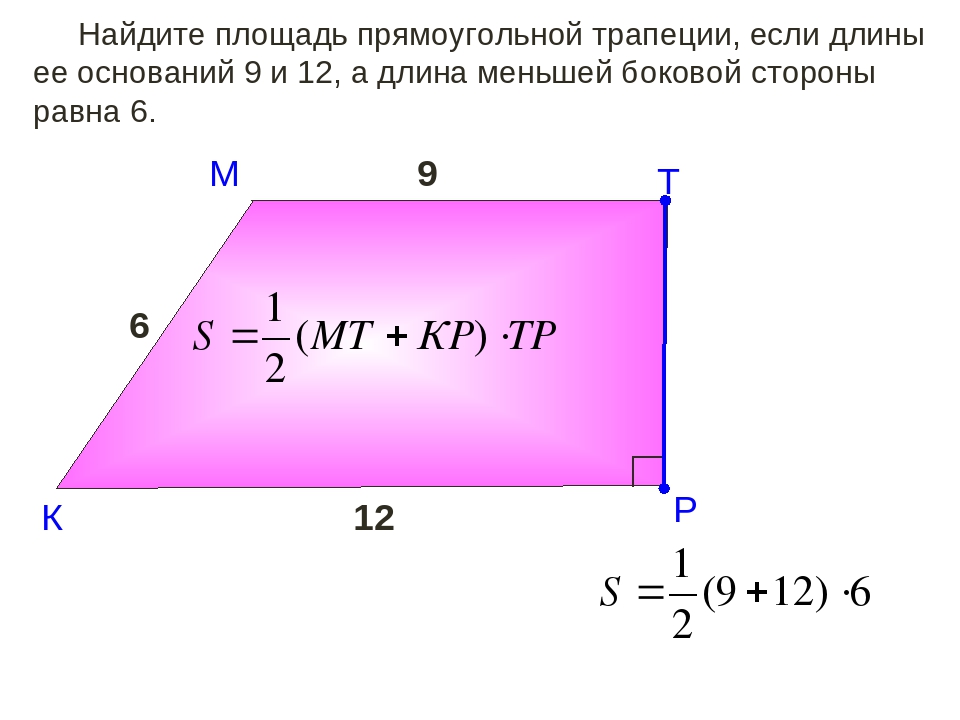
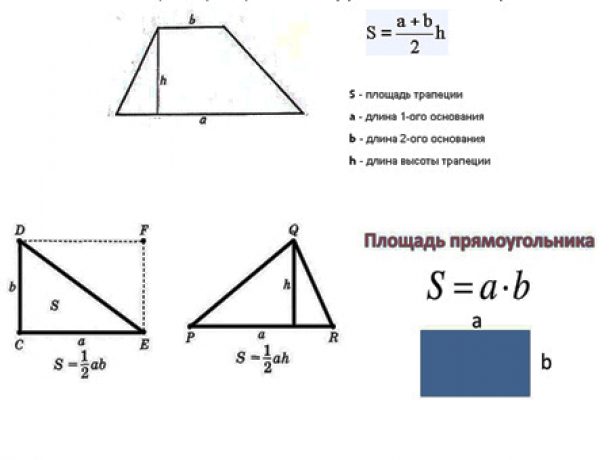
Если комната имеет формулу трапеции, то высчитать ее площадь можно без дележки помещения на простые фигуры. Формула трапеции вычисляется так: длина верхней границы (более короткой стороны – а) суммируется с длиной нижней границы (b), затем умножается на высоту трапеции (h) и полученный результат делится на два. Площадь четырехугольника с равными сторонами рассчитать можно по формуле: S = а (длина длинной стороны) х h (высота четырехугольника).
Расчет площадей разных геометрических фигур
Формулы расчетов
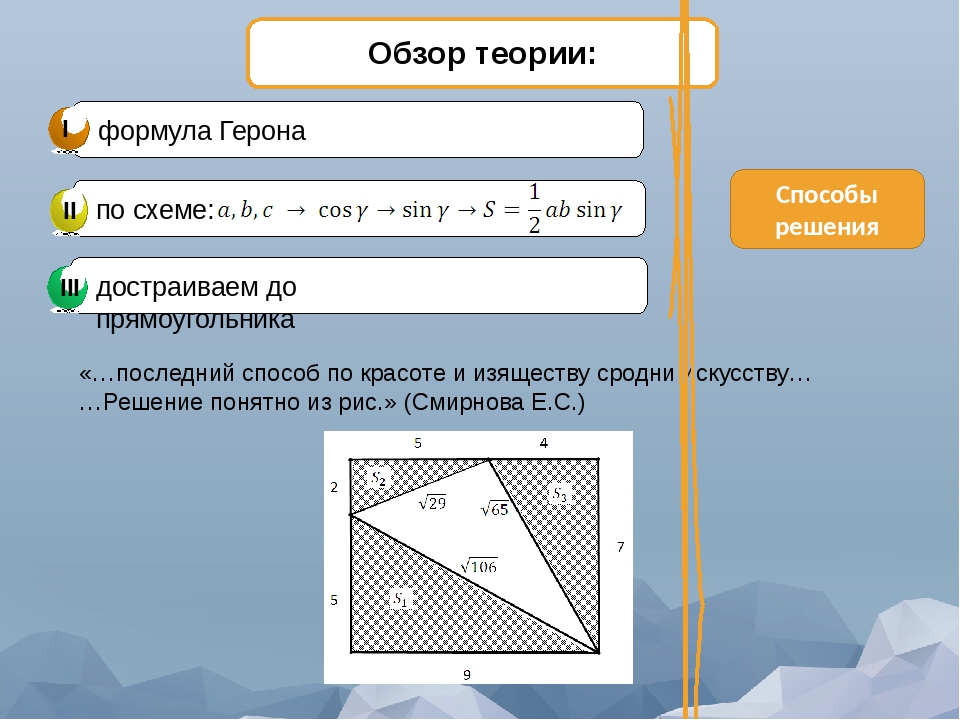
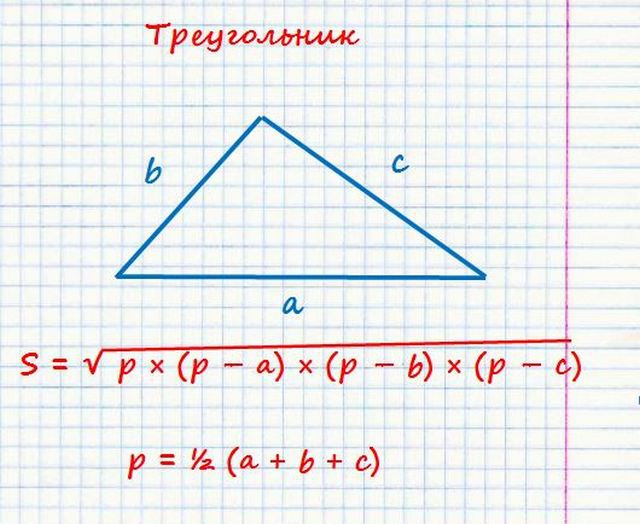
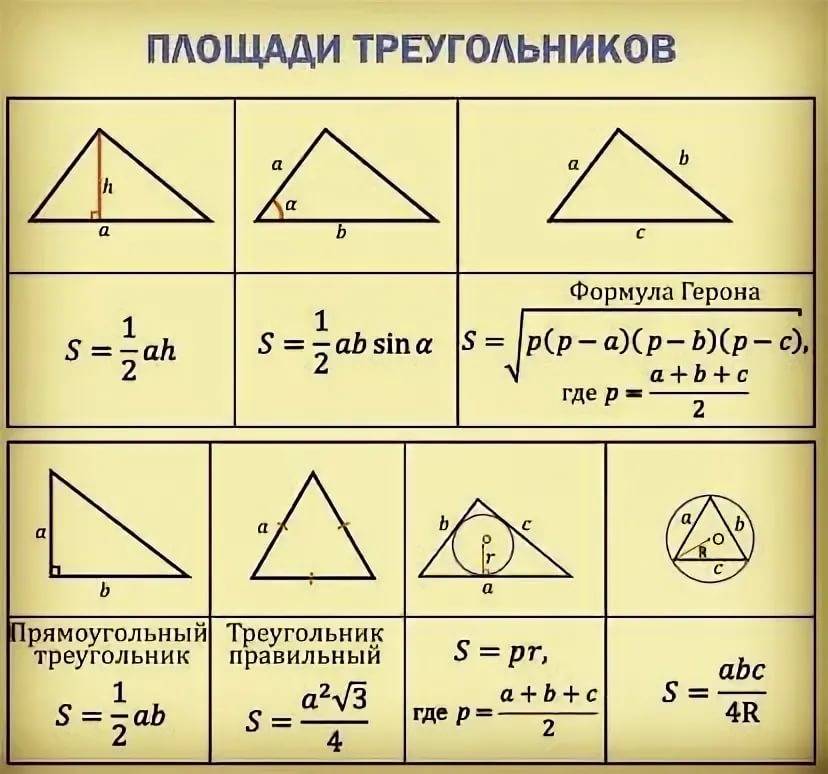
Если треугольник не прямой, то рассчитать его площадь можно с помощью формулы Герона
Площади усеченных частей круга
А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:
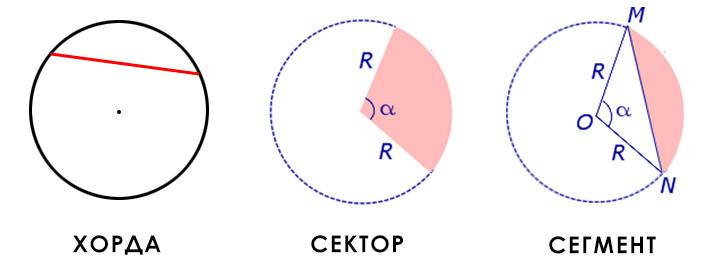
Хорда — отрезок, соединяющий любые две точки окружности.
Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.
Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:
где S — площадь сектора, r — радиус круга.
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.
Площадь сегмента можно найти по формулам:
где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.
Площадь круга и размеры пицц
Люди не всегда верно сопоставляют площадь круга и диаметры. К примеру, сможете ли вы ответить:
Интуитивно кажется, что 2 пиццы, так как в сумме их радиусы дают 50 сантиметров, что больше, чем 40. Однако это неправильный вывод, так как сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:
- 252 + 252 = 625 + 625 = 1250
- 402 = 1600
Так как ¼π является константой, то можно сравнивать только квадраты диаметров. Получается, что пицца 40 см больше, чем даже 2 пиццы размером 25 см. А вот если диаметр пиццы составляет 35 см, то 352 = 1225, и в этом случае 2 пиццы по 25 см будут иметь бОльшую площадь.
Площадь прямоугольного треугольника — формулы и калькуляторы
Прямоугольный треугольник — это треугольник, в котором один угол прямой (90°).
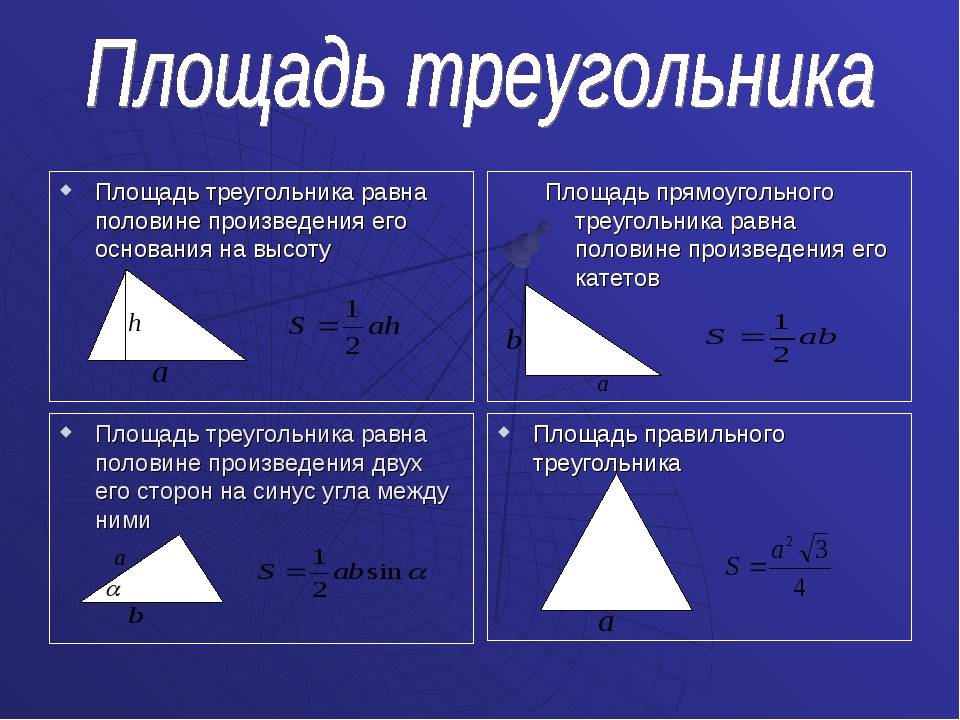
По основанию и высоте площадь прямоугольно треугольника равна половине произведения катетов треугольника.
Площадь прямоугольного треугольника по двум катетам — расчет:
| Формула | Результат |
| S = ½ × a × b | |
Катет a | |
Катет b |
Площадь прямоугольного треугольника через гипотенузу и угол:
| Формула | Результат |
| S = ¼ × c² × sin (2α) | |
Сторона c | |
Угол α |
Площадь прямоугольного треугольника через катет и угол — онлайн калькулятор:
| Формула | Результат |
| S = ½ × b² × tg (α) | |
Сторона b | |
Угол α |
Если в треугольник вписана окружность и известны отрезки, на которые она делит гипотенузу, то площадь прямоугольно треугольника равна произведению этих отрезков.
Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность:
| Формула | Результат |
| S = d × e | |
Отрезок d | |
Отрезок e |
Площадь прямоугольного треугольника через гипотенузу и вписанную окружность — расчет:
| Формула | Результат |
| S = r × (r + c) | |
Сторона с | |
Радиус r |
Площадь прямоугольно треугольника по трем сторонам (формула Герона) равна произведению разностей полупериметра треугольника и каждого из катетов. Полупериметр p = ½ × (a + b + c)
Площадь прямоугольного треугольника по формуле Герона:
| Формула | Результат |
| S = ( ½ × (a + b + c) — a) × ( ½ × (a + b + c) — b) | |
Сторона a | |
Сторона b | |
Сторона c |
Расчет площади
Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь треугольника.
Формула расчета
2. Через длину трех сторон (формула Герона)
Примечание: если результат равен нулю, значит отрезки с указанными длинами не могут образовывать треугольник (следует из свойств треугольника).
Формула расчета:
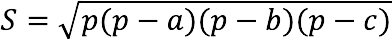
p – полупериметр, который считается так:
3. Через две стороны и угол между ними
Примечание: максимальный угол в радианах не должен быть больше 3,141593 (приблизительное значение числа π ), в градусах – до 180° (исключительно).
Площадь комнаты в квадратных метрах
Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:
- Рулетка. Лучше — с фиксатором, но подойдет и обычная.
- Бумага и карандаш или ручка.
- Калькулятор (или считайте в столбик или в уме).
Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.
Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.
Прямоугольная комната
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).
Как высчитать площадь комнаты
Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Помещение неправильной формы
Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.
Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.
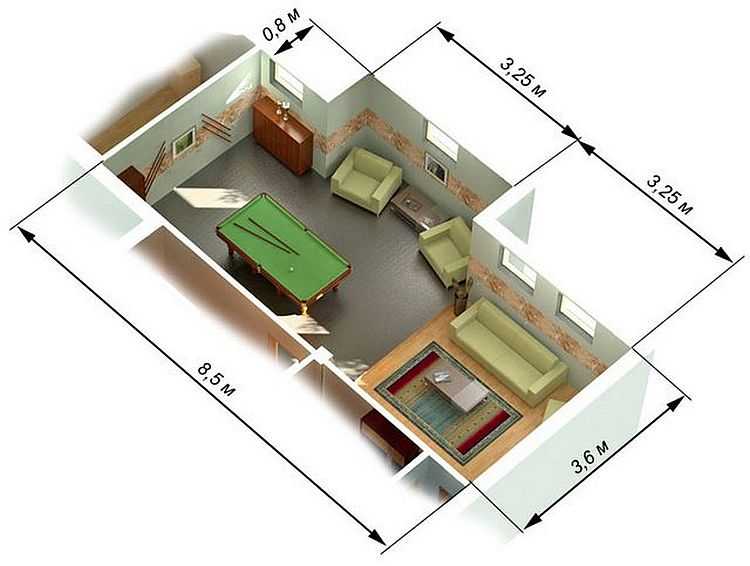Площадь комнаты сложной формы
Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):
- Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
- Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
- Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.
Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту
Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный. Как посчитать площадь комнаты неправильной формы
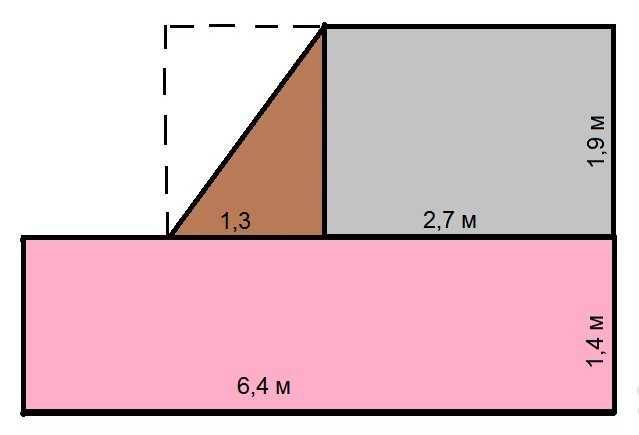Как посчитать площадь комнаты неправильной формы
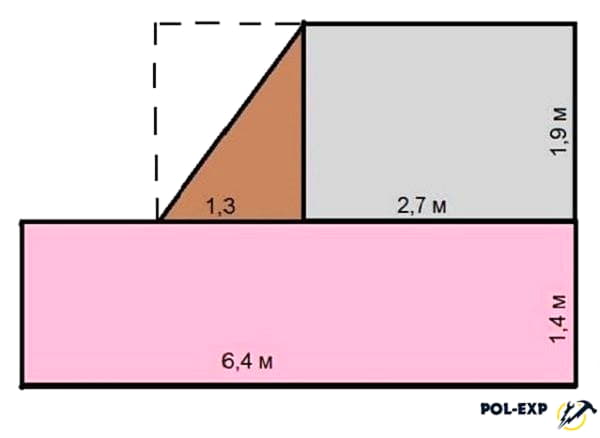
В этом случае порядок вычислений такой:
- Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
- Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
- Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
- Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.
Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.
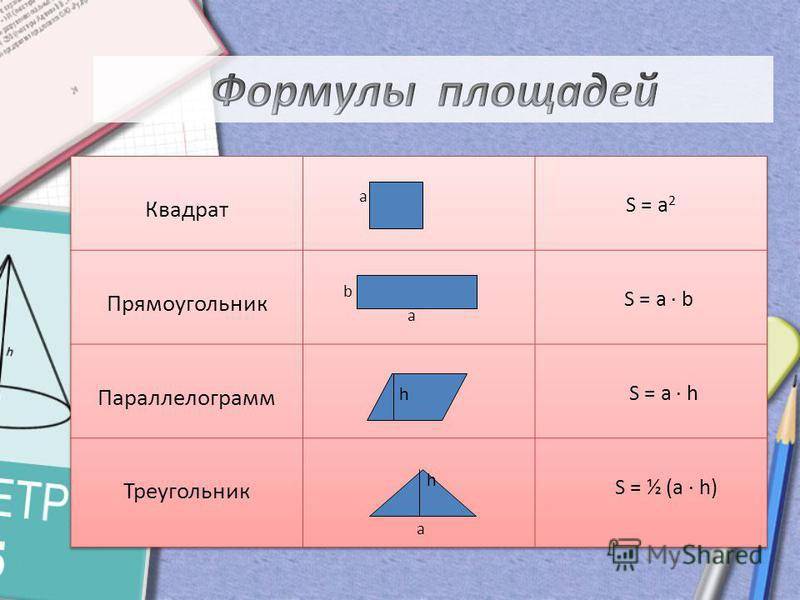
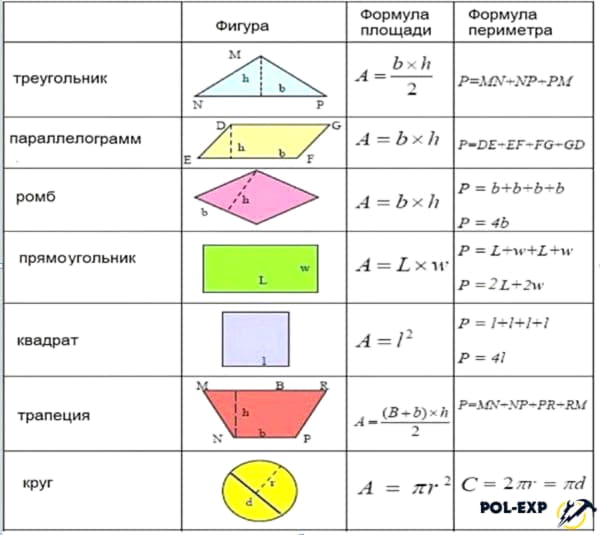
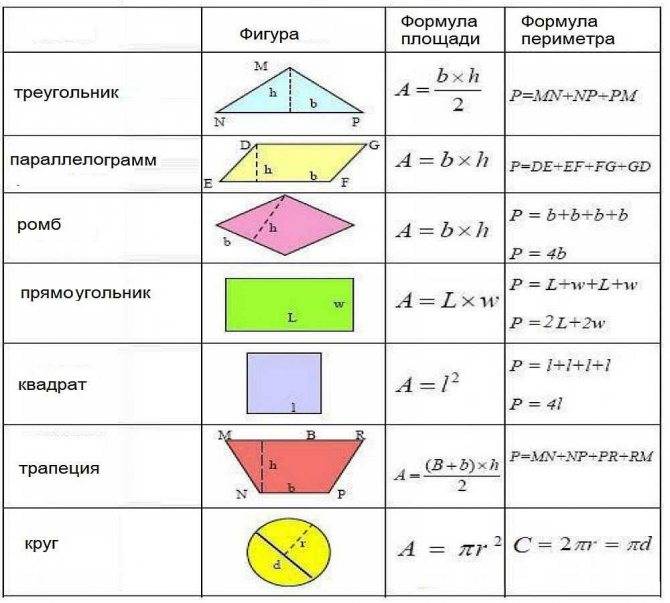Формулы расчета площади и периметра простых геометрических фигур
Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов
В результате получаем площадь пола
Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.
Считаем количество плитки
Зная площадь комнаты, рассчитать количество напольного покрытия будет несложно. Разберемся, как выяснить, сколько плитки понадобится для конкретной комнаты. Для этого нужно узнать, какова площадь одного элемента плиточного покрытия. Зная эти данные, легко произвести необходимые расчеты. Например:
- площадь комнаты – 15 м2;
- размер одной единицы плитки – 0,20х0,30 м.
Расчет количества плитки на пол
Таким образом, площадь одной плитки составит 0,2х0,3 = 0,06 м2. Далее общую площадь комнаты делим на площадь одной плитки и получаем: 15/0,06 = 250 единиц. Именно столько плиток потребуется, чтобы закрыть весь черновой пол в данном помещении. Точно таким же методом вычисляется и количество ламината или паркетной доски, а также других материалов.
Видео – Рассчитываем линолеум
Чтобы высчитать площадь пола в комнате, а затем – и расход материала, достаточно знать элементарные математические формулы и уметь пользоваться калькулятором. Имея последний под рукой (а сейчас калькулятор есть в каждом телефоне), произвести расчеты можно быстро. Главное – быть внимательными при снятии замеров.
Расчет площади пола в комнате неправильной формы
У комнат, имеющих неправильную форму, рассчитать площадь намного сложнее. Сложности добавляют такие элементы, как арки, ниши в форме полукруга, скошенные стены и т. д. По сути, принцип расчета тот же – нужно разбить помещение на несколько ровных фигур и высчитать площадь каждой отдельно, а потом суммировать. Но площадь круга или треугольника считается уже по другим формулам.
Пол неправильной формы
Например, площадь треугольника высчитывается так: длина основания умножается на высоту треугольника и делится на 2.
Расчет площади комнаты неправильной формы
На заметку! Проще всего по возможность делить все помещение на ровные фигуры типа квадратов и треугольников и считать их площади отдельно, а потом суммировать.
Площадь многоуровневых полос посчитать не так сложно, как кажется. Просто считаются площади отдельных сегментов и суммируются. Если ступени необходимо отделать таким же напольным материалом, как и остальной пол, то достаточно измерить площадь боковой части каждой ступени и приплюсовать к общей цифре.
Если комната имеет формулу трапеции, то высчитать ее площадь можно без дележки помещения на простые фигуры. Формула трапеции вычисляется так: длина верхней границы (более короткой стороны – а) суммируется с длиной нижней границы (b), затем умножается на высоту трапеции (h) и полученный результат делится на два. Площадь четырехугольника с равными сторонами рассчитать можно по формуле: S = а (длина длинной стороны) х h (высота четырехугольника).
Расчет площадей разных геометрических фигур
Формулы расчетов
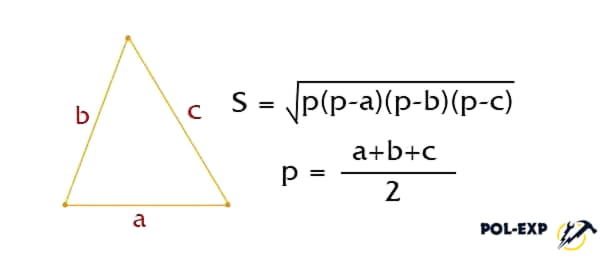
Если треугольник не прямой, то рассчитать его площадь можно с помощью формулы Герона
Как работает калькулятор площади треугольника?
Работа калькулятора площади треугольника может немного отличаться в зависимости от конкретного онлайн-инструмента, но обычно он использует формулу для расчета площади треугольника на основе заданных параметров.
Если треугольник является прямоугольным, то для расчета его площади необходимо знать длину основания и высоту, которая опускается на это основание. А если треугольник непрямоугольный, то для расчета его площади необходимо знать длины всех трех сторон.
Калькулятор площади треугольника может использовать эти формулы для расчета площади, если пользователь введет необходимые параметры (например, длины сторон или длину основания и высоту). Результат может быть выдан в виде числа или дроби в зависимости от точности калькулятора.
Площадь равносторонних треугольников — онлайн калькулятор, формулы
Правильный (равносторонний, или равноугольный) треугольник — это правильный многоугольник, все стороны которого равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
Площадь равностороннего треугольника по известной стороне равна произведению одной четвертой корня из трех на квадрат стороны.
Площадь равностороннего треугольника по стороне — онлайн расчет:
| Формула | Результат |
| S = ¼ × √(3) × a² | |
Сторона a (a = b = c) |
Если известна высота равностороннего треугольника, то его площадь равна отношению квадрата высоты к корню из трех.
Площадь равностороннего треугольника по высоте:
| Формула | Результат |
| S = h² ⁄ √(3) | |
Высота h |
Если известен радиус вписанной окружности, то площадь равностороннего треугольника равна произведению трех корней из трех на квадрат радиуса вписанной окружности.
Площадь равностороннего треугольника по радиусу вписанной окружности — калькулятор:
| Формула | Результат |
| S = 3 × √(3) × r² | |
Радиус r вписанной окружности |
По известному радиусу описанной окружности площадь равностороннего треугольника определяется, как произведение трех четвертей корня из трех на квадрат радиуса.
Площадь равностороннего треугольника по радиусу описанной окружности:
| Формула | Результат |
| S = ¾ × √(3) × R² | |
Радиус R описанной окружности |
Площадь треугольника — калькуляторы для всех видов
Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными. Рассмотренные в данном пункте калькуляторы и формулы подходят для всех видов треугольников.
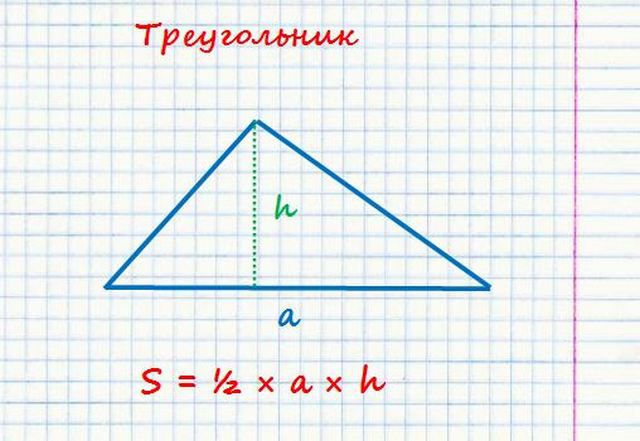
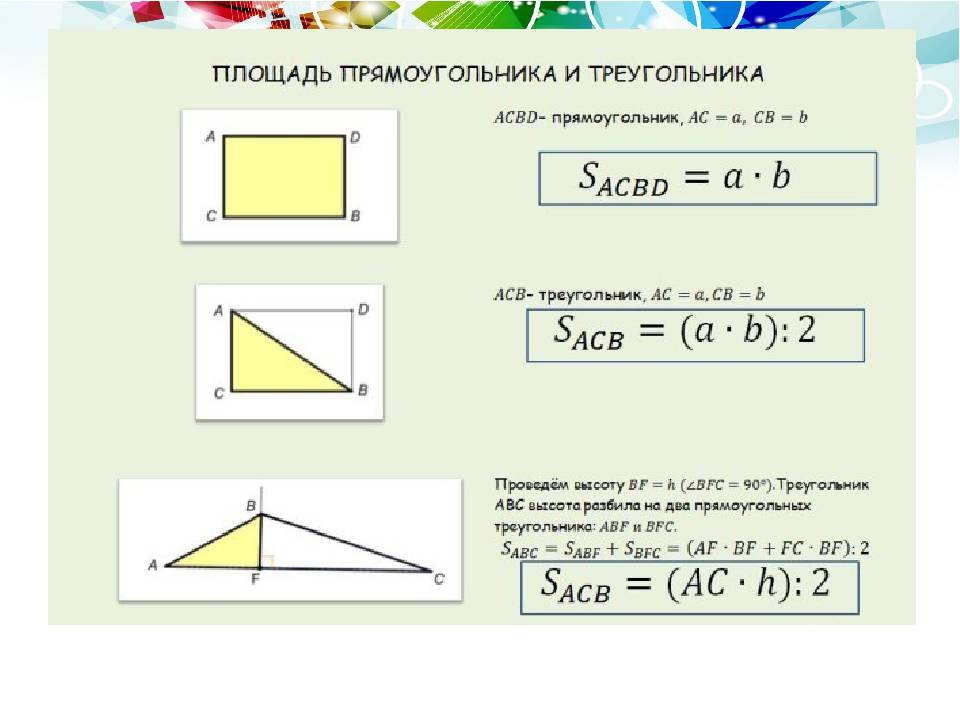
Зная сторону треугольника (основание) и высоту проведенную к основанию, можно найти его площадь. Площадь треугольника будет равна половине произведения основания на высоту. Основанием треугольника может быть выбрана любая из сторон треугольника.
Площадь треугольника по основанию и высоте — калькулятор онлайн:
| Формула | Результат |
| S = ½ × a × h | |
Сторона a | |
Высота h |
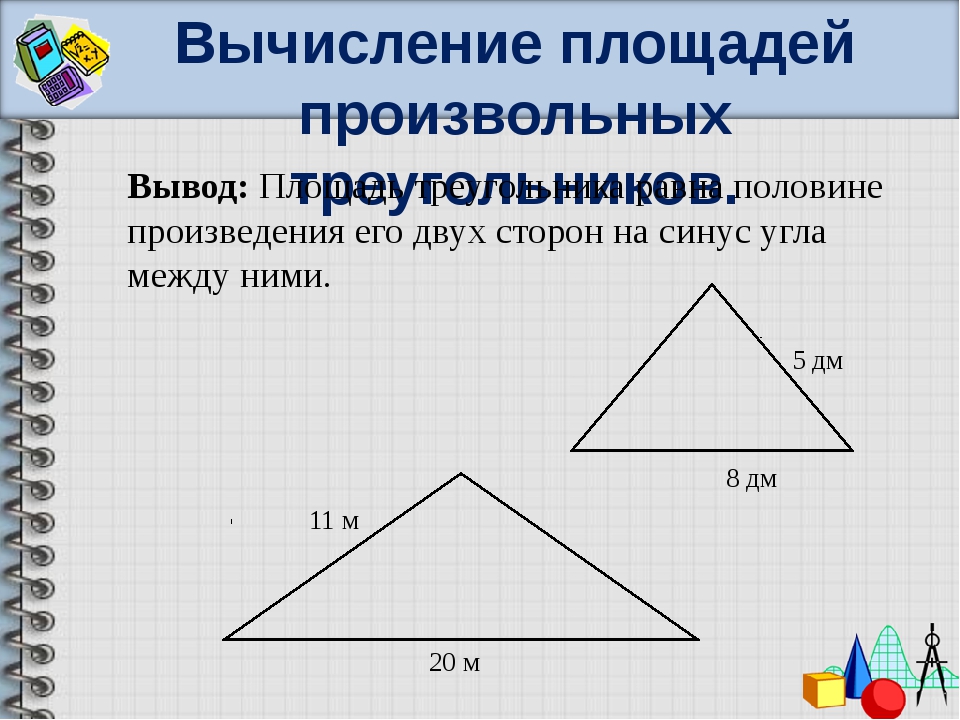
Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними. Угол α между сторонами может быть любым: тупым, острым, прямым.
Площадь треугольника по двум сторонам и углу между ними — расчет:
| Формула | Результат |
| S = ½ × a × b × α | |
Сторона a | |
Сторона b | |
Угол α° между сторонами a и b |
Если известно три стороны треугольника и радиус вписанной окружности, то площадь данного треугольника вычисляется, как половина суммы этих сторон (полупериметр p = ½ × (a + b + c)) умноженная на радиус вписанной окружности.
Площадь треугольника по радиусу вписанной окружности и трем сторонам — онлайн калькулятор:
| Формула | Результат |
| S = r × ½ × (a + b + c) | |
Сторона a | |
Сторона b | |
Сторона c | |
Радиус r вписанной окружности |
Если известно три стороны треугольника и радиус описанной окружности, то площадь треугольника равна частному от деления произведения сторон треугольника на четыре радиуса описанной около треугольника окружности.
Площадь треугольника по радиусу описанной окружности и трем сторонам — расчет:
| Формула | Результат |
| S = (a × b × c) ⁄ (4 × R) | |
Сторона a | |
Сторона b | |
Сторона c | |
Радиус R описанной окружности |
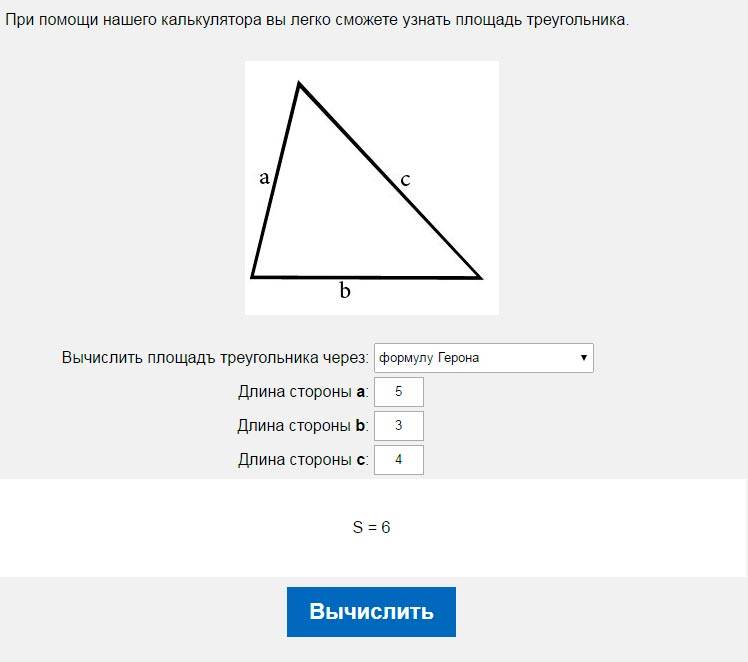
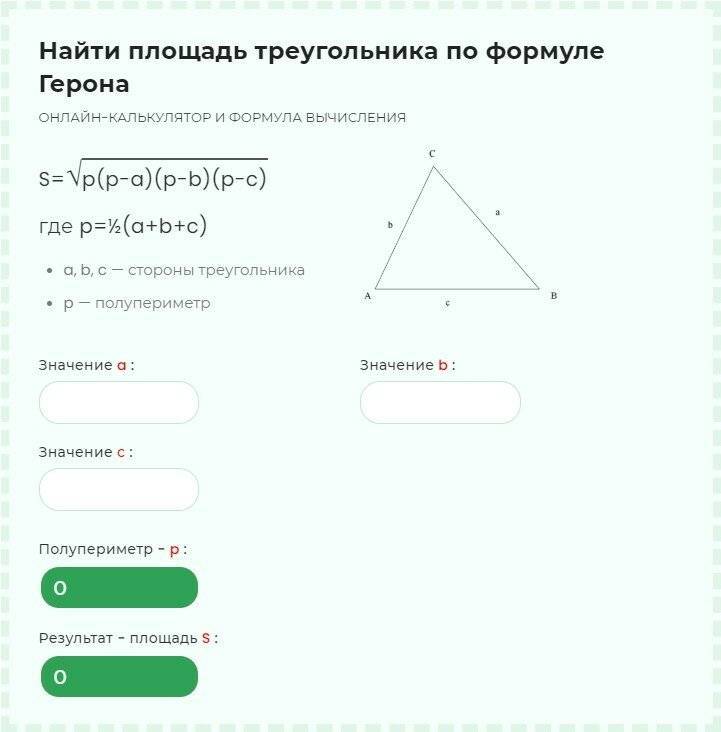
Площадь треугольника по формуле Герона равна корню из произведения разностей полупериметра треугольника (p) и каждой из его сторон (a, b, c) на полупериметр. Полупериметр p = (a + b + c) × ½.
Площадь треугольника по формуле Герона — калькулятор онлайн:
| Формула | Результат |
| S = √ p × (p — a) × (p — b) × (p — c) | |
Сторона a | |
Сторона b | |
Сторона c |
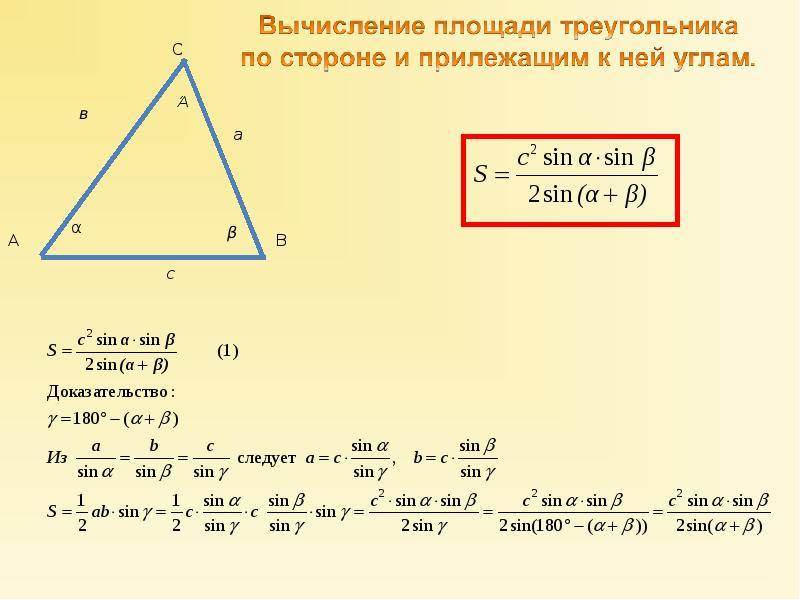
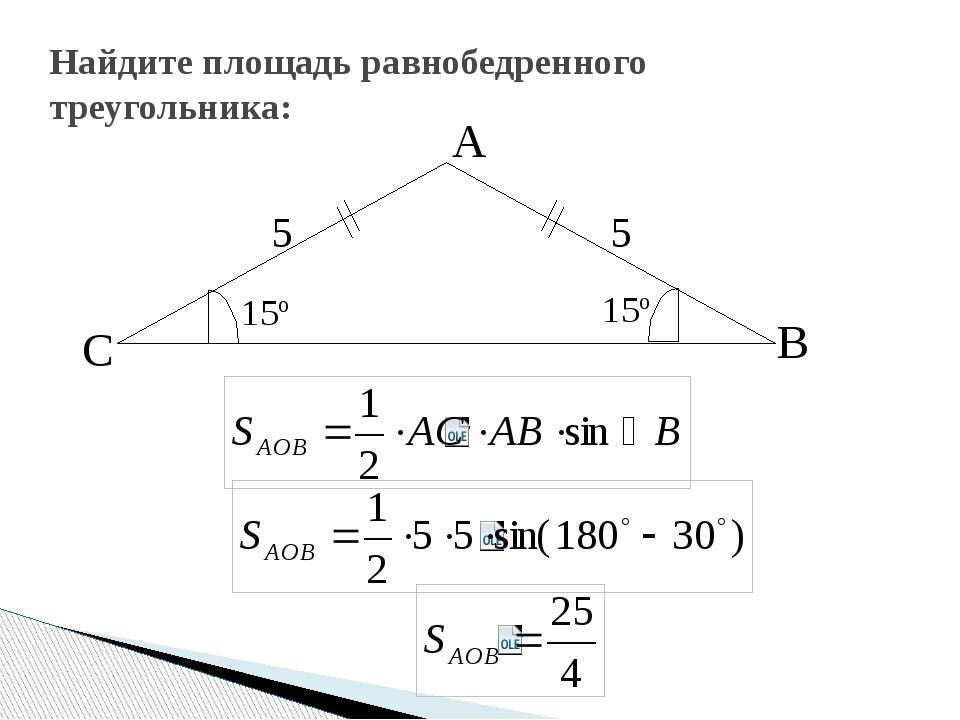
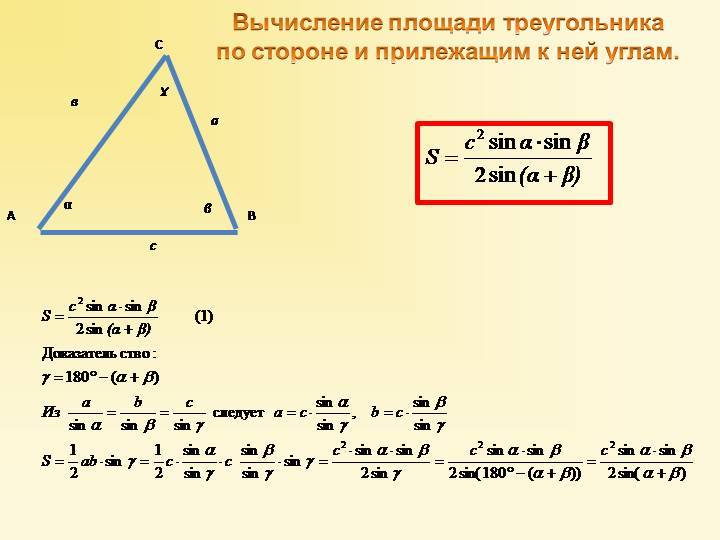
Площадь произвольного треугольника по стороне и двум прилежащим углам — расчет:
| Формула | Результат |
| S = ½ × a² × (sin α × sin β) ⁄ sin (180 — (α + β)) | |
Сторона a | |
Угол β° | |
Угол α° |
Как посчитать площадь стен
Какие бывают типы треугольников?
Есть много типов треугольников, каждый из которых имеет свои уникальные свойства. Треугольники часто делятся на следующие категории: равносторонние треугольники, равнобедренные треугольники и чешуйчатые треугольники. Понимание этих свойств поможет вам сформулировать свои собственные идеи в реальных приложениях.
Равносторонний треугольник
Равносторонний треугольник – это треугольник с тремя сторонами одинаковой длины.
Равнобедренный треугольник
Треугольник считается равнобедренным, если две стороны треугольника имеют одинаковую длину.
Неравносторонний треугольник
Разносторонний треугольник – это треугольник, у которого ноль равных сторон.
Виды треугольников
Как посчитать площадь комнаты в квадратных метрах
Важные моменты, которые нужно учесть перед проведением расчетов
Как посчитать площадь комнаты: методика расчета по полу
Можно рассчитать площадь пола. Данная процедура состоит из таких этапов. Прежде всего, необходимо освободить стены помещения. Лучше проводить измерения в пустом помещении. Если помещение прямоугольное, то можно перемножить две стороны
В реальности стороны могут немного отличаться, поэтому так важно мерить все стороны. В некоторых случаях комната может быть не правильной конфигурации
В такой ситуации все пространство делится на отдельные прямоугольники
При этом можно нарисовать схему со всеми размерами. Затем считается площадь отдельных участков. Кстати, помещение не обязательно будет состоять только из прямоугольников. Оно может содержать треугольники и даже круги
В такой ситуации все пространство делится на отдельные прямоугольники. При этом можно нарисовать схему со всеми размерами. Затем считается площадь отдельных участков. Кстати, помещение не обязательно будет состоять только из прямоугольников. Оно может содержать треугольники и даже круги.
В таблице можно посмотреть соответствие площади на полу с показателями для стен при определенной высоте потолка
Если вы не знаете, как посчитать квадратные метры комнаты, то можно воспользоваться специальным калькулятором. При вычислении габаритов не обязательно соблюдать все размеры до сантиметра. Часто применяется округление значений. Иногда требуется учитывать разные углубления и выступы в стенах.
При расчетах важно учитывать и их предназначение. Если нужно узнать значения для монтажа теплого пола, то можно не учитывать пространство, занятое тяжелой мебелью
Есть варианты, когда в помещении используются разные уровни пола
В подобной ситуации также требуется поделить комнату на отдельные зоны. Не стоит осуществлять замеры по стене, так как она может иметь кривую поверхность
Есть варианты, когда в помещении используются разные уровни пола. В подобной ситуации также требуется поделить комнату на отдельные зоны. Не стоит осуществлять замеры по стене, так как она может иметь кривую поверхность.
Сложно определить площадь по полу, имеющего разнообразные выступы в виде волн или полукругов.
Полы сложной конфигурации требуют особой внимательности и использования специальных формул
Измерения
Перед тем как измерить комнату в квадратных метрах, необходим минимальный набор предметов:
- калькулятор;
- рулетка;
- карандаш;
- лист бумаги.
На бумаге необходимо сделать подробный план помещения. Каждая стена должна быть измерена с использованием рулетки.
Вторым этапом является проставление полученных измерений на плане. Лучше всего сразу делать это в метрах, но точность каждого замера должна быть до 1 сантиметра. Это необходимо для того, чтобы при выборе необходимого количества материалов, удалось максимально точно подобрать метраж требуемого материала. Рулонные напольные покрытия продаются в погонных метрах.
Округлять можно только в случае небольшого увеличения, чтобы в случае непредвиденных обстоятельство, было достаточное количество материала.
Как высчитать квадратуру комнаты
Чтобы понять, как узнать общую площадь комнаты, необходимо воспользоваться простой формулой и перемножить показания длины на ширину. Как показано на рисунке длинная стена имеет длину в 7 метров а противоположная только 4. Выходит площадь пола будет равна 28 м2. Именно таким образом и находят квадратуру. Обязательно требуется помнить о небольшом запасе, который потребуется для подгонки и подрезки, причем чем сложнее будет вариант укладки, тем больше потребуется брать запас.
Пошаговый расчет площади комнаты
Шаг 1. Первым делом необходимо приготовить все измерительные инструменты, а также листок и ручку. На бумаге можно предварительно начертить схему комнаты, стараясь максимально сохранить геометрию и отобразить все ниши и детали помещения. Рулетка используется максимально длинная.
Подготовка всего необходимого
Шаг 2. Измеряется длина комнаты. Если она настолько велика, что рулетки не хватает, то замеры снимаются поэтапно. Для начала производится замер на максимальную длину рулетки, в месте ее окончания делается отметка, от которой потом снова производится замер до конца комнаты.
Для начала нужно измерить длину комнаты
Шаг 3. Измеряется ширина комнаты (вдоль стены с меньшей длиной). Рулетка располагается под прямым углом к ранее измеряемой стене комнаты (длине). Полученные данные записываются.
Измеряется ширина комнаты
Шаг 4. Полученные показатели перемножаются между собой. Для этих целей рекомендуется использовать калькулятор. При необходимости значение площади округляется в большую сторону.
Полученная цифра округляется в большую сторону
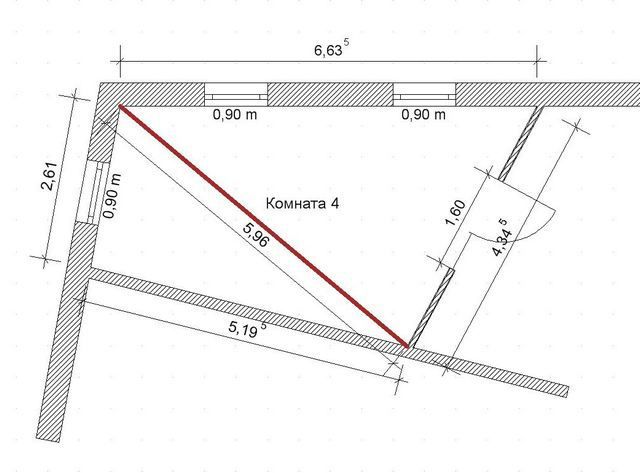
Шаг 5. Если необходимо измерить площадь сложной геометрически комнаты, то для начала сложная фигура делится на несколько простых – квадратов, треугольников, прямоугольников. Объект изображается на листочке бумаги схематически, схематически делится.
Комната разделена на 4 прямоугольника
Шаг 6. Производится замер каждой фигуры в отдельности. Например, прямоугольники, треугольники.
Каждая фигура замеряется отдельно
Шаг 7. Производится вычисление площади каждой фигуры. Далее все полученные значения суммируются и получается полная точная площадь пола комнаты.
Пример расчета площади треугольника
Как правильно рассчитать площадь стен со сложной поверхностью
Не все помещения имеют строгую прямоугольную форму. В зданиях часто присутствуют замысловатые архитектурные элементы, усложняющие расчет.
Как посчитать квадратуру стен за вычетом проемов
При определении точного объема работ, вычтем размеры окон и дверей из общего количества квадратных метров стен комнаты. Для этого по краю рамы замеряем ширину и высоту окна, по краю коробки — габариты двери.
Перемножив длину и ширину проемов, получаем размер, который необходимо вычесть.
Аналогично действуем, если из подсчитываемой квадратуры комнаты нужно исключить печи, камины, радиаторы.
Пример:
В помещении имеется окно 2,5 м × 1,5 м и дверь 0,9 м × 2,1 м.
S окна равна 2,5 × 1,5 = 3,75 м².
S двери равна 0,9 × 2,1 = 1,89 м².
S стен за вычетом проемов составляет 54 − 3,75 − 1,89 = 48,36 м².
Определение площади помещений неправильной формы
Для определения периметра зданий любых конфигураций сложим длины всех стен, включая выступы и ниши.
Рисунок 1. Элемент с выступом.
Проводить измерения помещений неправильной формы можно, разбив поверхность на несколько простых фигур.
Если у вас комната с прямоугольным выступом, вы имеете две фигуры, квадратуру которых легко вычислить, затем сложить.
Если элемент содержит в себе полукруг, для расчета нужно разбить его на полукруг и прямоугольник.
Рисунок 2. Элемент с полукругом.
Как считать квадратные метры стен с круглыми элементами
Встречаются круглые и полукруглые жилые здания или строения с элементами окон или дверей в виде арки.
Их периметр можно определить, умножив диаметр на число π (Пи) = 3,14.
Квадратуру вертикальных поверхностей определяем, умножив полученное значение на высоту от пола до потолка.
S круга равна квадрату радиуса, умноженному на число π; полукруга — половине этой величины.
Если необходимо из квадратуры комнаты вычесть площадь круглых колонн или полукруглых выступающих элементов, при невозможности измерить диаметр или радиус, измеряем длину окружности (P) и применяем формулу: S = P² / 4π.
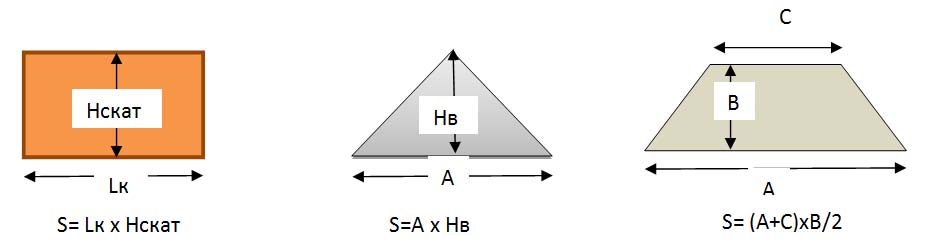
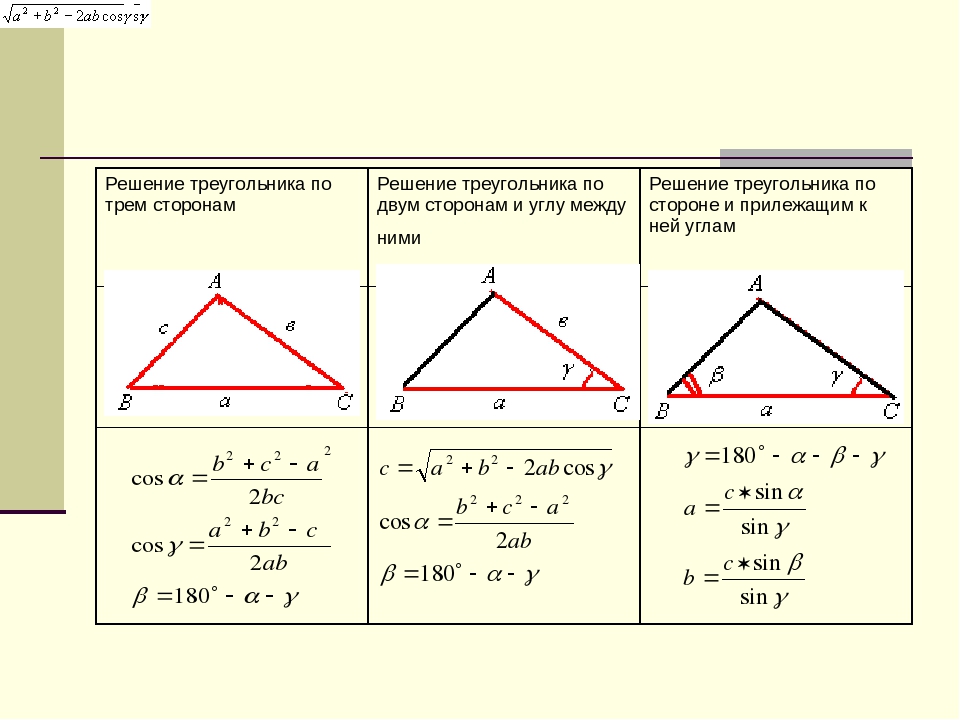
Как рассчитать квадратные метры конструкций в виде треугольника
В случае наличия комнаты с треугольными элементами, мы можем применить несколько формул, в зависимости от вида фигур:
Рисунок 3. Формулы определения площади треугольников.
Где a, b, c — длины сторон треугольника; p — периметр.
Объем помещения
Для определения объема необходимо высчитать площадь пола, и полученный показатель перемножить на высоту. V = S × h.
Как рассчитать площадь треугольника?
Площадь треугольника – это общее пространство, занимаемое его тремя сторонами. Основная формула расчета его площади равна основанию и высоте треугольника.
Площадь треугольника по высоте и основанию
Triangle area = (height * base) / 2
Площадь треугольника также можно рассчитать разными способами с помощью углов и длин треугольника.
Площадь треугольника по трем сторонам
Triangle area = 1/4 * √( (a + b + c) * (-a + b + c) * (a – b + c) * (a + b – c) )
Площадь треугольника по двум сторонам и угол между ними
Triangle area = 1/2 * a * b * sin(γ)
Площадь треугольника на два угла и сторона между ними
Triangle area = a^2 * sin(β) * sin(γ) / (2 * sin(β + γ))
Какие инструменты применяют для расчета площадей?
Для расчета площади комнаты можно использовать различные компьютерные программы, также применяются различные математические формулы для вычислений. Но размеры сторон геометрической фигуры, которой соответствует помещение, снимать придется в любом случае.
Таблица. Инструменты для снятия размеров комнаты.
| Наименование | Рекомендации |
|---|---|
Бумага и ручка/карандаш | Необходимы для записи полученных показаний. Если показания не записывать, то можно быстро запутаться. Также бумага и пишущие принадлежности пригодятся для составления плана помещения. |
Рулетка | С ее помощью и определяются непосредственно все размеры. Чем больше комната, тем длиннее рулетку придется приобрести. Не стоит использовать мягкую тканевую сантиметровую ленту, которой пользуются закройщики – она достаточно короткая и мягкая, потому снимать мерки будет неудобно и можно допустить погрешности. |
Калькулятор | Необходим для совершения всех математических операций. Удобен тем, что позволит снизить риск возникновения погрешностей. |
Лазерный дальномер | Удобный прибор, который позволит быстро и точно снять мерки любого помещения. |
Угольник, транспортир | Может понадобиться для измерения углов в помещении. Стоит помнить, что даже кажущиеся прямыми углы не всегда бывают такими. А порой знать точный размер угла необходимо. |
Расчет вручную на листочке удобен тем, что все параметры можно тут же перемерить на месте и внести необходимые коррективы. Но ошибиться при ручном способе расчетов довольно просто, поэтому лучше лишний раз пересчитать все показатели.
Для автоматического подсчета площади помещения удобно использовать различные графические редакторы. Это могут быть AutoCAD, ArchiCAD или SketchUP. В них создается фигура по форме комнаты, размеры всех ее сторон указываются при создании макета. Площадь комнаты будет выдана программой автоматически и с высокой точностью (вплоть до сантиметров и миллиметров). Все будет зависеть от точности снятых мерок. Особенно использование этих программ рекомендуется, если необходимо высчитать площадь комнаты, сложной по своей геометрии. Недостатком этого метода является необходимость хотя бы поверхностного изучения программ, а также использование компьютерной техники.
Пример использования программы SketchUP
Расчет площади
Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь треугольника.
Формула расчета
2. Через длину трех сторон (формула Герона)
Примечание: если результат равен нулю, значит отрезки с указанными длинами не могут образовывать треугольник (следует из свойств треугольника).
Формула расчета:
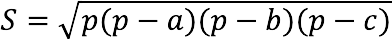
p – полупериметр, который считается так:
3. Через две стороны и угол между ними
Примечание: максимальный угол в радианах не должен быть больше 3,141593 (приблизительное значение числа π ), в градусах – до 180° (исключительно).
❓Вопросы и ответы
Также полезно ознакомиться с ответами на часто задаваемые вопросы по данному вопросу.
Как использовать калькулятор площади треугольника?
Для использования калькулятора площади треугольника нужно ввести известные параметры треугольника, такие как длины сторон, длина основания и высота, координаты вершин на плоскости и т.д., а затем нажать на кнопку «Рассчитать» или «Вычислить». Калькулятор автоматически рассчитывает площадь треугольника и выводит результат.
Какой формулой рассчитывается площадь треугольника?
Площадь треугольника можно рассчитать с помощью формулы: S = (a * h) / 2, где S – площадь треугольника, a – длина основания, h – высота, опущенная на основание.
Где можно найти онлайн-калькулятор площади треугольника?
Онлайн-калькуляторы площади треугольника можно найти на многих сайтах, которые предоставляют подобные сервисы. Также можно использовать калькуляторы научных порталов или мобильные приложения.
Какие единицы измерения используются в калькуляторе площади треугольника?
Калькулятор площади треугольника может использовать разные единицы измерения, например, метры, сантиметры, дюймы, футы и т.д. Обычно единицы измерения выбираются в соответствии с системой измерений, используемой в конкретной стране или регионе.
Расчет площади помещения с несколькими уровнями
Думаете, что таких комнат не бывает? Совершенно напрасно, дом, построенный на склоне, вполне может иметь в планировке уступы, например, так гостиная или кухня может быть поделена на зоны. Впрочем, совершенно не обязательно смотреть на пол, ведь и потолок может состоять из нескольких ярусов в самом обычном типовом помещении. Допустим, вам нужно купить краску для его окраски. Разумеется, в целом площади потолка и пола равны, но вот в местах перепада высот вертикальные откосы тоже имеют некоторую квадратуру. И даже с учетом 10 % запаса к закупаемым материалам их может не хватить. Поэтому считаем.
Если уровни у вас простой формы, с прямоугольными элементами, никаких сложностей не возникнет. Достаточно измерить линейкой высоту вертикальных участков, найти их длину и, использовав формулу S = a . b, определить площадь, с которой суммируется квадратура горизонтальных поверхностей. Если край уступа нависает над более низкой площадкой в виде карниза, суммировать результаты измерений каждого яруса недостаточно, поскольку получится, что не учтена нижняя сторона нависающей части. Для настилания паркета или облицовки плиткой эти места особой роли играть не будут, а вот при окраске могут остаться «белые пятна». Так что при подобном положении дел следует обмерить линеечкой и скрытые участки.
Обмеры рулеткой или иным приспособлением лучше выполнять ближе к основанию, поскольку стены могут иметь небольшую кривизну, что даст определенную погрешность в результате.
Сложнее всего выполнять расчет площади помещения при наличии уступов округлой или более сложной формы. В этом случае нужно точно измерить каждую дугу по краю, либо короткими отрезками, либо сразу целиком посредством рулетки и воспользовавшись чьей-нибудь помощью. Затем, найдя радиусы и раздробив поверхности на отдельные геометрические фигуры, используем приведенные выше формулы и находим площадь каждого уступа. Что касается вертикальных участков, о них также было сказано выше, разницы между прямым вариантом и изогнутым нет никакой, если известен периметр.
