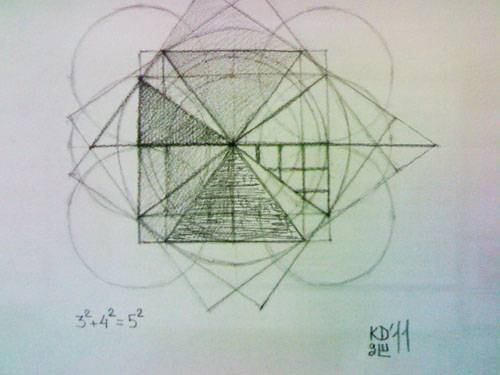
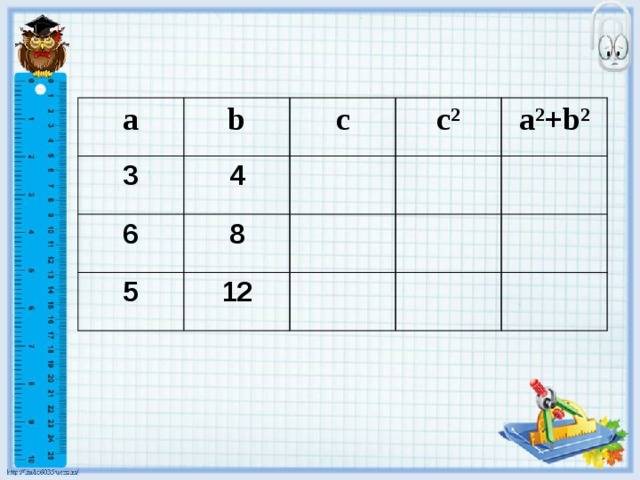
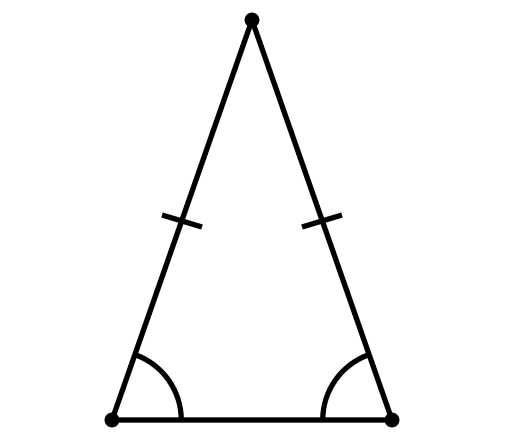
Египетский треугольник в строительстве. Общие сведения
Зарождение идеи
Идея у математика появилась после путешествия в Африку по просьбе Фалеса, который поставил задачу Пифагору изучить математику и астрономию тех мест. В Египте он среди бескрайней пустыни встретил величественные строения, поразившие его размером, изяществом и красотой.
Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.
Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.
Из истории
Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.
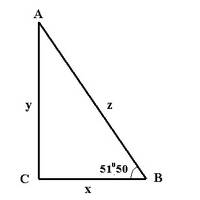
Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала пирамида Хеопса, отличающаяся совершенными пропорциями. Ее место особенное в истории. Если посмотреть поперечное сечение, то можно отметить два треугольника, у которых угол внутри равняется 51о50’.
Строение
 Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.
Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.
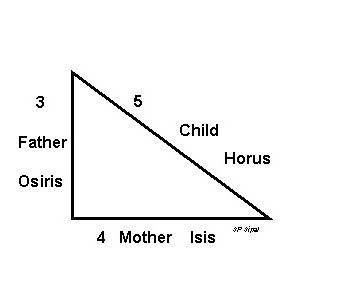
Однако, следует рассмотреть другую пирамиду – Хефрена, у которой основа как раз-таки прямоугольный треугольник и где угол наклона боковых граней равен 53о12 с соотношением катетов 4:3. Это уже так называемый священный треугольник. Для египтян такая фигура сопоставлялась с семейным очагом: катет вертикального положения олицетворял мужчину, основание – представительницу прекрасного пола, а гипотенуза – рождение ребенка от обоих.
Стороны пирамиды Хефрена в соотношении равны 3:4:5, что точно соответствует теореме Пифагора. Значит, можно сделать вывод, что строители уже знали об этой теореме, но не могли ее сформулировать. Хотя, в исторических письменах встречаются следы использования египетского треугольника за много веков даже до Египта. До сегодняшнего дня это загадка, как могли такие знания получить древние египтяне. Понимали ли они чем обладают?
Особенность фигуры к тому же в том, что благодаря подобному соотношению, она является простым и первым Героновым треугольником, так как ее стороны и площадь целочисленные.
Обратное доказательство
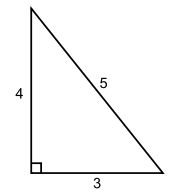
Как доказать, что треугольник прямоугольный? Нужно порой исходить от обратного, то есть если сумма квадратов обеих сторон равна квадрату третьей, то треугольник прямоугольный, что подтверждает равенство 32х42=52 и значит он действительно прямоугольный.
Таким образом теорема Пифагора стала каноном и фундаментом развития математической науки. Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».
Интересно, что теорема Пифагора находится в Книге Гиннесса как теорема, обладающая самым большим количеством доказательств, которых примерно 500.
Особенности
Если рассмотреть более детально отличительные особенности египетского треугольника, то можно выделить следующие моменты:
- все стороны и площадь состоят из целых чисел, как говорилось выше;
- согласно теории великого математика, сумма квадратов катетов равна квадрату гипотенузе;
- такой фигурой возможно отмерить прямые углы в пространстве. Это используется в процессе строительства до сих пор;
- не обязательно пользоваться специальными измерительными приборами, подойдут подручные средства, например, веревка.
Египетский треугольник в строительстве
Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.
Важно! Конечно, в идеале лучшим вариантом будет использование транспортира или угольника. Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы
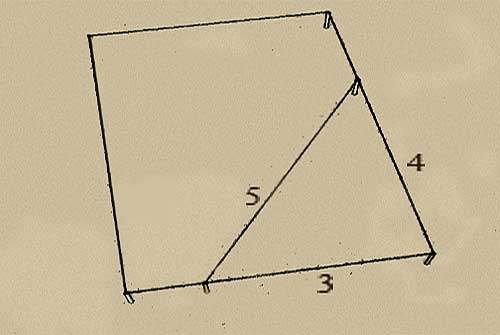
Стороны конструкции имеют следующее соотношение друг к другу:
Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:
- 5,
- 4,
Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.
Внимание! Свойства египетского треугольника таковы, что квадрат гипотенузы равен квадратам двух катетов. Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример
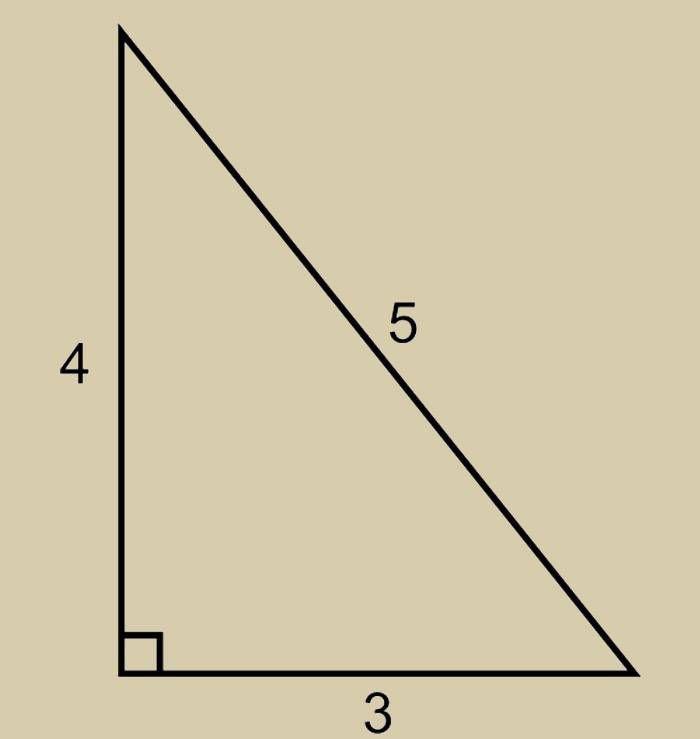
Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять
Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.
Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.
Внимание! Длина каждого отрезка составит 4 и 3 см (при минимальных значениях). Пересечение этих прямых образует прямой угол, равняющийся 90 градусам
Альтернативные способы построить прямой угол на 90 градусов
Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.
Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.
Как получить египетский треугольник при помощи верёвки
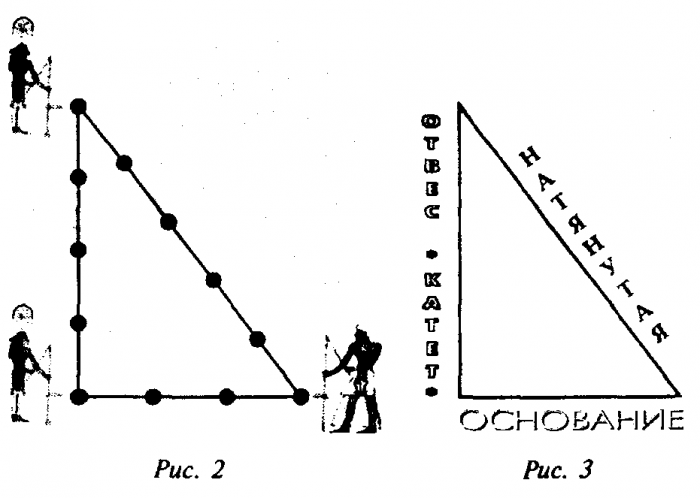
Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.
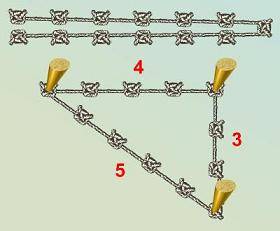
Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.
Как построить угол в 45, 30 и 60 градусов
Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.
Важно! Для получения нужного наклона вырвите лист бумаги из журнала и согните его. При этом линии изгиба будут проходить через угол
Края должны совпасть.
Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.
Внимание! Соотношение сторон на 30º нужно, чтобы сделать шестиугольники. Их свойства востребованы в столярных заготовках
Какие существуют альтернативные варианты
Как создать прямой угол
Лучшим вариантом смастерить прямой угол является применение угольника или транспортира. Это позволит с минимальными затратами найти необходимые пропорции. Но, основной момент египетского треугольника в его универсальности из-за возможности создать фигуру, не имея под рукой ничего.
В этом деле может пригодиться все, даже печатные издания. Любая книга или даже журнал имеют всегда соотношение сторон, образующее прямой угол. Типографские станки работают всегда точно, чтобы рулон, заправленный в машину резался пропорциональными углами.
Древние инженеры придумывали много способов строительства египетского треугольника и всегда экономили ресурсы.
Поэтому, самым простым и широко применяемым был метод постройки геометрической фигуры с применением обычной веревки. Бралась бечевка и резалась на 12 ровных частей, из которых выкладывалась фигура с пропорциями 3,4 и 5.
Как создать другие углы?
Египетский треугольник в строительном мире нельзя недооценивать. Его свойства однозначно полезны, но без возможности построить углы другого градуса в строительстве невозможно. Чтобы образовался угол в 45 градусов, понадобится рамка или багет, которые распиливаются под углом в 45 градусов и соединяются между собой.
Важно! Чтобы получить необходимый наклон, потребуется позаимствовать бумажный лист из печатного издания и согнуть его. Линии изгиба при этом будут проходить через угол
Края должны быть соединены.
Получить 60 градусов можно с применением двух треугольников по 30 градусов. Чаще всего используются для создания декоративных элементов.
Как треугольник используется в строительстве?
Треугольник используется в строительстве, чтобы убедиться, что что-то квадратное или что-то квадратное. Квадрат скорости представляет собой небольшой треугольный инструмент, используемый для обозначения углов стропила. Один из методов проверки квадрата комнаты или одной стены, перпендикулярной другой, состоит в том, чтобы измерить 3 фута вдоль одной стены и сделать отметку карандашом, чтобы они измеряли 4 фута вдоль другой стены и делали метку карандаша. Затем измерьте диагонально от метки карандаша до метки карандаша. Если число составляет 5 футов, две стены квадратные друг к другу.
Глаз в треугольнике
Символ, графически представляющий собой вписанный в треугольник глаз, называемый «глазом провидения» или «всевидящим оком», появился в Европе в XVII в. Считается, что он восходит к солярному глазу Гора древних египтян. Этот знак получил широкое распространение в барочной архитектуре, украшая фронтоны роскошных католических костелов.
В XIX в. он появился и на православных храмах, например, на фронтоне Казанского собора в Санкт-Петербурге. Христианство рассматривало его как символ Святой Троицы. Одновременно этот символ использовался и масонами, которые трактовали его как символ абсолюта, просвещения и высшего знания. У масонов «глаз провидения» располагается над стулом мастера ложи, чтобы таким образом напоминать о всепроникающей во все тайны мудрости Творца.
 Декларация прав человека и гражданина, Франция, конец XVIII в.
Декларация прав человека и гражданина, Франция, конец XVIII в.
 Герб белорусского города Браслав
Герб белорусского города Браслав
Египетский треугольник и обратная теорема Пифагора
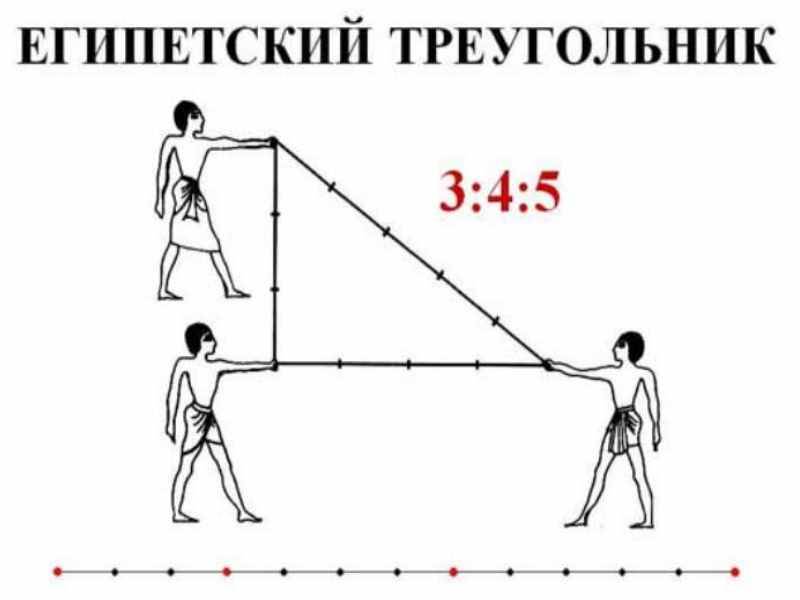
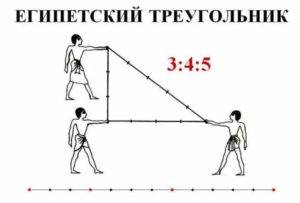
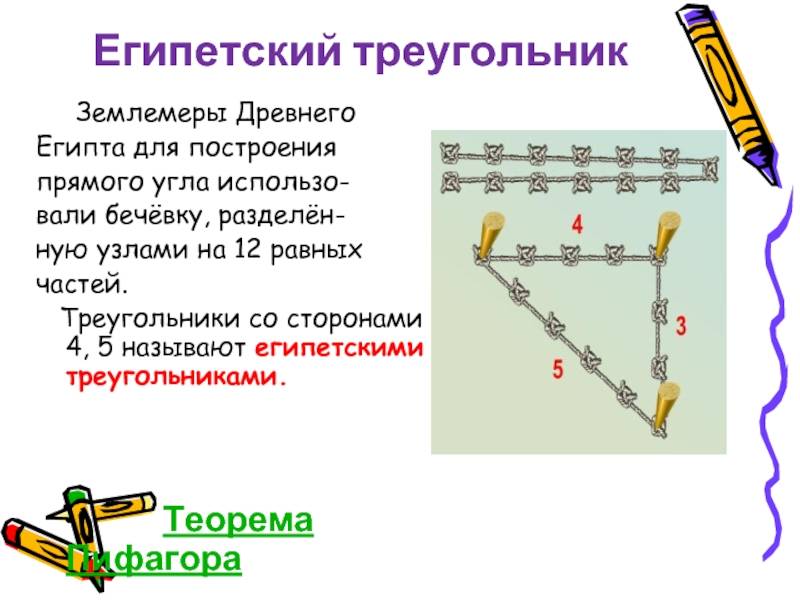
Математический лайфхак из обасти геометрии “Как при помощи простой верёвки получить треугольник с прямым углом”. Египтяне 4000 лет назад для строительства пирамид использовали метод получения прямоугольного треугольника при помощи верёвки разделенной на 12 равных частей.
Понятие “египетский треугольник”.
Почему треугольник со сторонами 3, 4, 5 называют египетским?
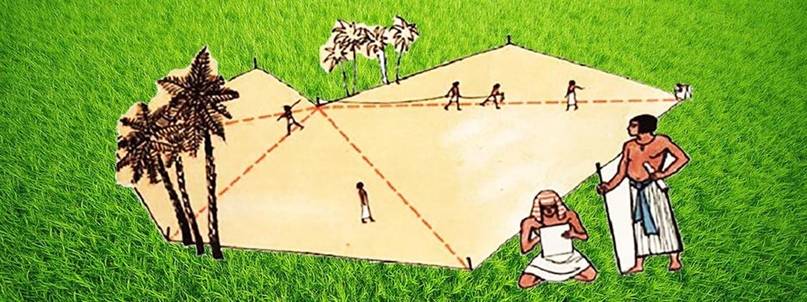
А всё дело в том, что строителям Древнего Египта пирамид нужен был простой и надежный метод построения треугольника с прямым углом. И вот как они это реализовывали. Верёвку разбивали на двеадцать равновеликих частей, обозначив границы между соседними частями; концы верёвки соединяли. После этого 3 человека натягивали верёвку таким образом, чтобы она образовала треугольник, причем расстояния между каждыми двумя египтянами, тянущими веревку, составляли соответственно три части, четыре части и пять частей. Получался треугольник с прямым углом с катетами в три и четыре части и гипотенузой в пять частей. Известно, прямым был угол между сторонами в три и четыре части. Как известно, древнеегипетских землемеров, которые кроме обмеривания земельных наделов занимались построениями на местности, в древнем Египте их называли гарпедонаптами (что буквально переводится как «натягивающие верёвки»). Гарпедонапты занимали 3 место в иерархии жрецоы Древнего Египта.
Обратная теорема Пифагора.
Но из-за чего треугольник со сторонами 3, 4, 5 окажется прямоугольным? Большинство ответили бы на данный вопрос, что данный факт это теорема Пифагора: так как три в квадрате плюс четыре в квадрате равняется пяти в квадрате. Но теорема Пифагора говорит, что если треугольник с прямым углом, то тогда сумма квадратов 2-х его сторон равняется квадрату третьей. Здесь мы имеем дело с теоремой, обратной теореме Пифагора: если сумма квадратов 2-х сторон треугольника равна квадрату третьей, то тогда треугольник — прямоугольный.
Обрисованное практическое приложение обратной теоремы Пифагора относиться к далёкому прошлому. Едва ли кто-либо получает прямые углы таким методом сегодня. Но тем не менее данный способ является отличным математическим лайфхаком и может быть применён Вами в любой жизненной ситуации.
Стороны египетского треугольника обладают удивительным свойством. Этот удивительный египетский треугольник.
Ка-ж-дый, кто внимательно слушал в школе преподавателя геометрии, очень хорошо знаком с тем, что представляет собой египетский треугольник. От других видов подобных с углом в 90 градусов он отличается особым соотношением сторон. Когда человек впервые слышит словосочетание «египетский треугольник», на ум приходят картины величественных пирамид и фараонов. А что же говорит история?
У Апокалипсиса есть одержимость как ветхозаветными, так и новозаветными библейскими отрывками, фиксация, которая чаще встречается в масонстве, где объединены библейские и египетские идеи. Апокалипсис умирает, говоря «Все раскрывается», что не имеет смысла в фильме, но говорит с аудиторией, говоря, что скрытые знания или секреты масонов выходят из публики и больше не скрываются.
Боб говорит, что Апокалипсис создает пирамиду в современный день, используя свою способность перемещать материю. Способность укладывать материю на молекулярном уровне для формирования любой компоновки или конструкции материи в любой форме или форме, проявленной с помощью современных специальных эффектов, может быть секретом, который он утверждает, «раскрывается», когда он говорит «Все раскрыто». Пирамида и построение сознания Древних Строителей и Масонов должны представлять высший интеллект над звериной природой нормального человечества.
Как это всегда бывает, в отношении названия «египетский треугольник» есть несколько теорий. Согласно одной из них, известная теорема Пифагора увидела свет именно благодаря данной фигуре. В 535 году до н.э. Пифагор, следуя рекомендации Фалеса, отправился в Египет с целью восполнить некоторые пробелы в познаниях математики и астрономии
Там он обратил внимание на особенности работы египетских землемеров. Они очень необычным способом выполняли построение с прямым углом, стороны которой были взаимосвязаны одна с другой соотношением 3-4-5
Данный математический ряд позволял относительно легко связать квадраты всех трех сторон одним правилом. Именно так и возникла знаменитая теорема. А египетский треугольник как раз и есть та самая фигура, натолкнувшая Пифагора на гениальнейшее решение. Согласно другим историческим данным, фигуре дали название греки: в то время они часто гостили в Египте, где могли заинтересоваться работой землемеров. Существует вероятность, что, как это часто бывает с научными открытиями, обе истории произошли одновременно, поэтому нельзя с уверенностью утверждать, кто же придумал первым название «египетский треугольник». Свойства его удивительны и, разумеется, не исчерпываются одним лишь соотношением размеров сторон. Его площадь и стороны представлены целыми числами. Благодаря этому применение к нему теоремы Пифагора позволяет получить целые числа квадратов гипотенузы и катетов: 9-16-25. Конечно, это может быть простым совпадением. Но как в таком случае объяснить тот факт, что египтяне считали «свой» треугольник священным? Они верили в его взаимосвязь со всей Вселенной.
Концептуальное искусство Ральфа МакКуэрри для «Звездных войн» довольно простое, когда оно адаптировано к фильму, но есть одно изображение, которое, как представляется, является видом на землю Облачного города, с городом из трех основных пирамид, окруженных более мелкими пирамидами. Этот образ никогда не попадал в кино.
Как вы можете встать, если вы не на коленях? Исаак Вайшаупт был на переднем крае теорий заговора, связанных с неуловимым «Иллюминатами» и его проникновением в индустрию развлечений. Это исследования теорий с использованием людей и событий в качестве демонстраций. Автор не знает, связаны ли эти люди с этими практиками, а изучает их поведение, чтобы получить теорию. Если кто-то здесь, как утверждается, является частью «Иллюминатов», пожалуйста, не принимайте его как факт, пока вы не выполните собственное исследование.
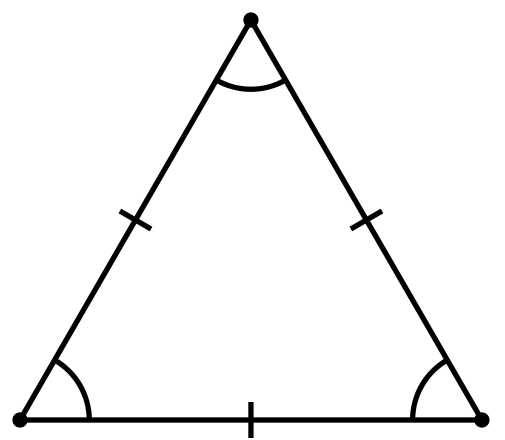
Правый треугольник имеет один угол, равный 90 градусам. Правый треугольник также может быть равнобедренным треугольником, что означает, что он имеет две стороны, которые равны. Правый равнобедренный треугольник имеет угол 90 градусов и два угла 45 градусов. Это единственный правильный треугольник, который является равнобедренным треугольником. Эта версия правого треугольника настолько популярна, что пластиковые модели из них изготавливаются и используются архитекторами, инженерами, плотниками и художниками-графиками в их проектных и строительных работах.
О египетском треугольнике и его свойствах хорошо известно ещё с древних времён. Эта фигура широко применялась в строительстве для разметки и построения правильных углов.
История египетского треугольника
Создателем этой геометрической конструкции является один из величайших математиков древности Пифагор. Именно благодаря его математическим изысканиям мы можем в полной мере использовать все свойства данного геометрического построения в строительстве.
Действительно, есть некоторые египетские рисунки, на которых найден такой инструмент. Имеются данные о том, что пифагорейская теорема была известна также и вавилонянам. Отсюда можно сделать вывод, что они также могли выполнять вычисления с прямоугольным треугольником, по крайней мере в некоторых случаях.
Основываясь на нынешнем уровне знаний об египетской и вавилонской математике и древних греческих источниках, Ван дер-Варден сделал следующий вывод. Достоинство первых греческих математиков, таких как Фалес, Пифагор и Пифагорейцы, – это не открытие математики, а ее систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных идеях, стали наукой.
Можно предположить, что математические навыки позволили Пифагору заметить закономерность в формах строения. Дальнейшее развитие событий можно легко представить. Базовый анализ и построение выводов создали одну из самых значимых фигур в истории. Скорее всего, в качестве прообраза была выбрана именно пирамида Хеопса из-за своих практически совершенных пропорций.
Геометрия у индейцев, а также у египтян и вавилонян была тесно связана с культами. Весьма вероятно, что квадрат гипотенузы был известен в Индии около 18 г. до н.э. Это разные фразы теоремы Пифагора в переводе с древнегреческого, латинского и немецкого языков.
В Евклиде эта теорема гласит. «В прямоугольном треугольнике квадрат стороны пролива над прямым углом равен квадратам сторон, которые фиксируют правый угол». Латинский перевод арабского текста ананиритов был сделан Герхардом Клемонским. «В каждом прямоугольном треугольнике квадрат, сформированный сбоку, нарисованный над прямым углом, равен сумме двух квадратов, сформированных с обеих сторон, покачиваясь под прямым углом».
Справочная информация
ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной
Египетский треугольник
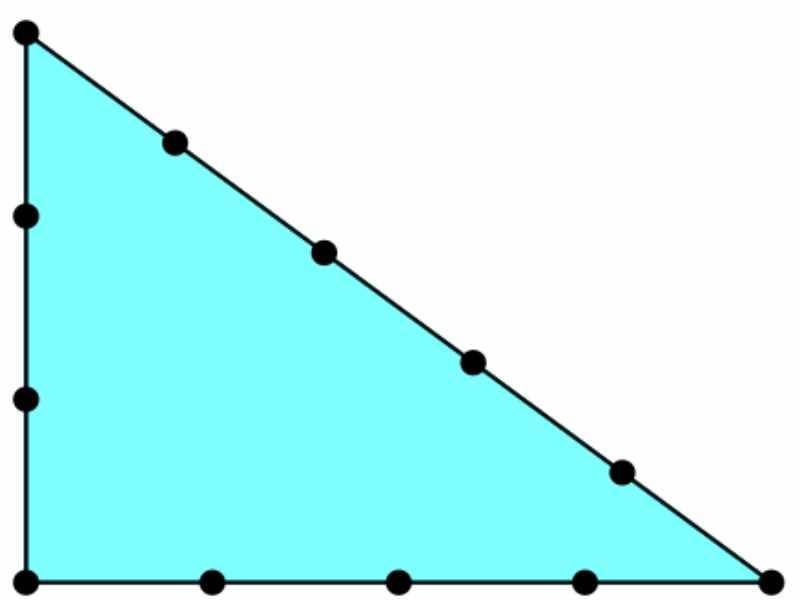
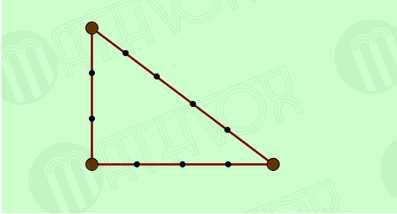
Египетский треугольник – прямоугольный треугольник с соотношением сторон 3:4:5. Сумма указанных чисел (3+4+5=12) с древних времен использовалась как единица кратности при построении прямых углов с помощью веревки, размеченной узлами на 3/12 и 7/12 ее длины. Применялся египетский треугольник в архитектуре средних веков для построения схем пропорциональности.
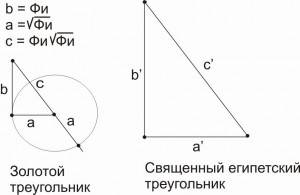
Итак, с чего же начать? Разве вот с этого: 3 + 5 = 8. а число 4 составляет половину числа 8. Стоп! Числа 3, 5, 8… Разве они не напоминают что-то очень знакомое? Ну конечно, они имеют прямое отношение к золотому сечению и входят в так называемый «золотой ряд»: 1, 1, 2, 3, 5, 8, 13, 21… В этом ряду каждый последующий член равен сумме двух предыдущих: 1 + 1= 2. 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8 и так далее. Выходит, что египетский треугольник имеет отношение к золотому сечению? И древние египтяне знали, с чем имели дело? Но не будем торопиться с выводами. Необходимо выяснить детали поточнее.
Выражение «золотое сечение», как считают некоторые, впервые ввел в XV веке Леонардо да Винчи. Но сам «золотой ряд» стал известен в 1202 году, когда его впервые опубликовал в своей «Книге о счете» итальянский математик Леонардо Пизанский. Прозванный Фибоначчи. Однако почти за две тысячи лет до них золотое сечение было известно Пифагору и его ученикам. Правда, называлось оно по-другому, как «деление в среднем и крайнем отношении». А вот египетский треугольник с его «золотым сечением» был известен еще в те далекие времена, когда строились пирамиды в Египте, когда процветала Атлантида.
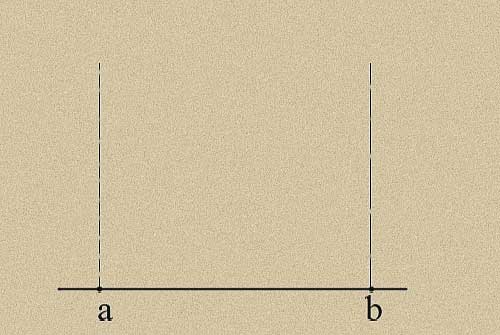
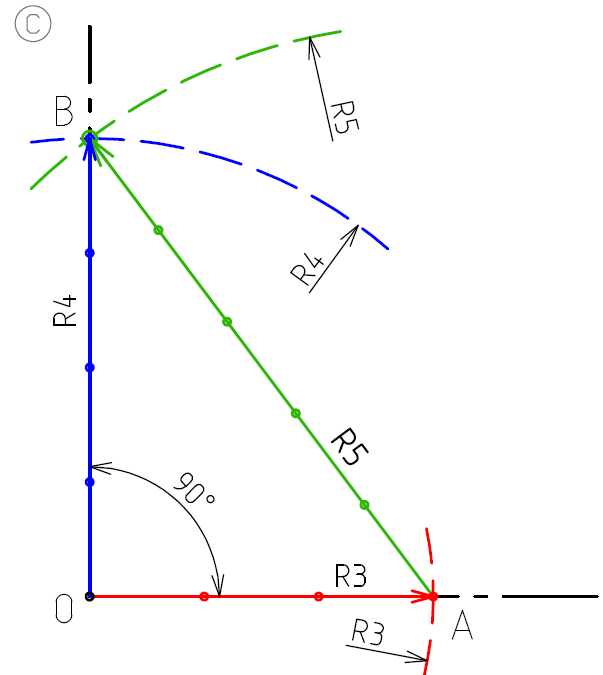
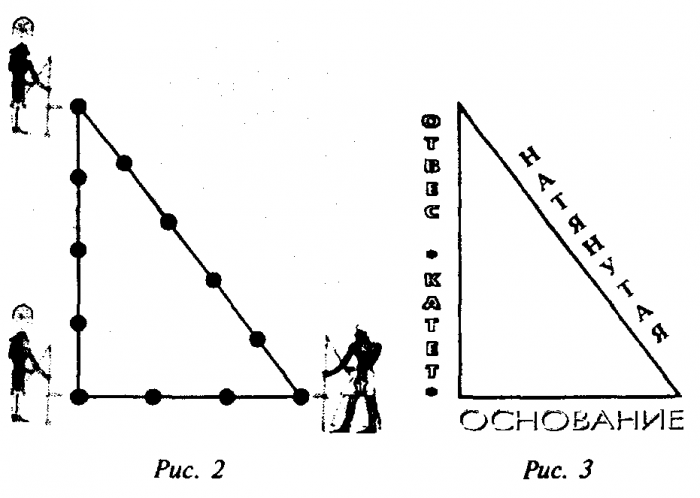
Для доказательства теоремы о египетском треугольнике необходимо использовать отрезок прямой известной длины А-А1 (рис.). Он будет служить масштабом, единицей измерения, и позволит определить длину всех сторон треугольника. Три отрезка А-А1 равны по длине наименьшей из сторон треугольника ВС, у которой соотношение равно 3. А четыре отрезка А-А1 равны по длине второй стороне, у которой соотношение выражается числом 4. И, наконец, длина третьей стороны равна пяти отрезкам А-А1. А дальше, как говорится, дело техники. На бумаге проведем отрезок ВС, являющийся наименьшей стороной треугольника. Затем из точки В радиусом, равным отрезку с соотношением 5, проводим циркулем дугу окружности, а из точки С —дугу окружности радиусом, равным длине отрезка с соотношением 4. Если теперь точку пересечения дуг соединить линиями с точками В и С, то получим прямоугольный треугольнике соотношением сторон 3 : 4 : 5.
Что и требовалось доказать.
Глупая ошибка строителей
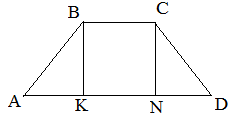
«Египетский треугольник» действительно может помочь в разметке периметра фундамента, однако применение этого метода требует сохранения чётких пропорций. Небольшое отклонение от них − и угол уже не будет прямым. А это приведёт к разнице длин стен. Не единичны случаи, когда при идеальном совпадении длин диагоналей стены получаются разными. Ведь если вдуматься, то трапеция также подходит под заданные параметры, её диагонали равны, в то время как верхняя и нижняя сторона имеют разные длины.
 ФОТО: youc.irПравильная трапеция также имеет одинаковые длины диагоналей, однако на квадрат она явно не тянет
ФОТО: youc.irПравильная трапеция также имеет одинаковые длины диагоналей, однако на квадрат она явно не тянет
Место в строительном мире
С древнейших времен египетский треугольник нашел почетное место в архитектуре и строительстве. Конструкция пирамиды отличается тем, что позволяет создавать здание с совершенно правильными углами без каких-либо дополнительных инструментов.
Задача намного облегчается, если использовать транспортир или треугольник. Но, раньше применялись только шнуры и веревке, разделенные на отрезки. Благодаря отметкам на веревке можно было с точностью воссоздать прямоугольную фигуру. Строителям заменяла транспортир и угольник веревка, для чего отмечали узлами на ней 12 частей и складывали треугольник с отрезками 3,4,5. Прямой угол получался без затруднений. Эти знания помогли создать множество сооружений, в том числе пирамиды.
Интересно, что до древнего Египта, таким способом строили в Китае, Вавилоне, Месопотамии.
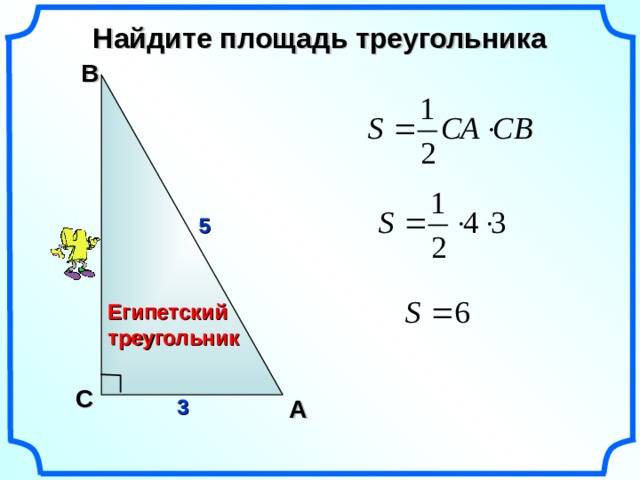
Свойства египетской треугольной фигуры подчиняются истине – квадрат гипотенузы равен квадратам двух катетов. Эта теорема Пифагора знакома каждому со школьной поры. Например, умножаем 5х5 и получаем гипотенузу равную числу 25. Квадраты обоих катетов равны 16 и 9, что в сумме дает цифру 25.
Благодаря таким свойствам, треугольник нашел применение в строительстве. Можно взять любую деталь, с целью провести линию прямого направления с условием, что ее длина должна быть кратной пяти. После этого заметить один край и прочертить от него линию кратную четырем, а от другого кратную трем. При этом каждый отрезок должен быть длиной минимум четыре и три. Пересекаясь, они образовывают один прямой угол в 90 градусов. Другие углы равны 53,13 и 36,87 градусам.
Прямой угол при строительстве. Нужна лишь веревка и помощь египтян.
При любой стройке часто сталкиваешься с проблемой разметки прямого угла на местности. Несомненно, что существуют всевозможные лазерные приборы, которые эту проблему решают на раз два. Они удобны и практичны. Но имеют один существенный недостаток — цена. Если вы профессионал — тогда — да, этот прибор незаменим. Ну а если любитель, и нужно всего пару раз построить прямой угол, то лишние расходы не к чему. Всегда можно обойтись веревкой, как делали с незапамятных времен. Даже египетские пирамиды строили с помощью этого способа и это до сих пор не потеряло актуальности.
Есть метод, который вполне рабочий и основан он на школьной геометрии. Допустим вам нужно поставить, грубо говоря, столбы под прямым углом друг к другу(угол забора). Этот способ я применял, когда делал на своем участке стол и вбивал трубы в землю. Конечно можно было и на глаз, но так как с этим у меня всегда была беда, то воспользовался обычной веревкой. Главное в этом, чтоб она не растягивалась, вот и все. У меня под рукой оказался мягкий тонкий провод, что вполне подходило под эти задачи.
Суть основывается на, так называемых, египетских треугольниках. Их еще называют Героновыми, Евклидовыми, Пифагоровыми. Не будем вдаваться в подробности, отмечу лишь, что зачастую египетские — это частное от всех остальных. Лишь Пифагоровы тройки точно отвечают нашим требованиям.
Вот этот замечательный треугольник. Его стороны являются целым числом, что нам и нужно. Соответственно. Берем веревку и строим с помощью нее эту фигуру на земле. И не обязательно откладывать именно 3 метра, 4 и 5. Самое главное — соблюсти пропорции. За единицу измерения можно взять и полметра, а можно и любую другую удобную длину. Для примера — полуметровые соотношения — 1,5 м 2 м и 2,5 м. Просто, чем больше размеры — тем точнее наши построения.
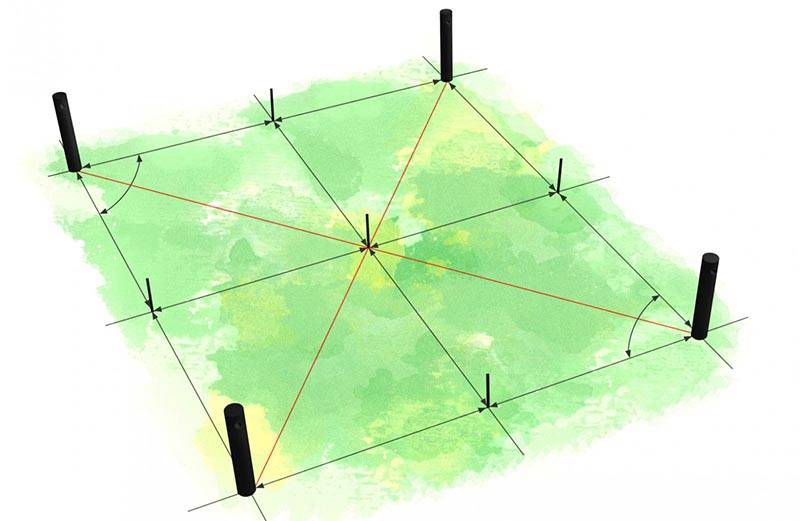
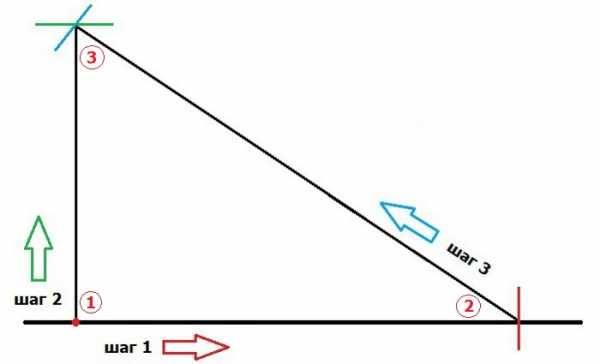
Итак. Забиваем столб, от которого нам и надо построить прямой угол. От него отмечаем 3 метра и забиваем колышек на этом месте. К колышку привязываем веревку в пять метров а к столбу — четырехметровую. Связываем свободные концы друг с другом и натягиваем веревки, чтобы обе ни где не провисали. Когда найдем это место — туда колышек и все. Построения закончены — прямой угол у нас имеется. А дальше по линиям веревки забиваем столбы на нужном нам расстоянии.
Просто, дешево, быстро. Главное в этом деле — не спешить, и чем больше точность в отрезках веревки — тем ближе угол к 90 градусам.
Кстати, есть еще пару методов на основе треугольников и знаний геометрии, но об этом как нибудь в следующий раз. А на этом пока все.