Как найти периметр прямоугольника?
Ниже в статье вы узнаете что такое и как найти периметр прямоугольника если известны его стороны. А также как найти стороны прямоугольника, если известен его периметр. И ещё одна интересная строительная прикладная задача.
Немного теории:
Периметр — это длина геометрической фигуры по её внешней границе.
Периметр прямоугольника — это сумма длин его сторон.
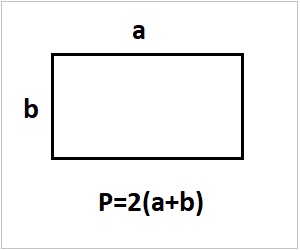
Формулы для вычисления периметра прямоугольника: P = 2*(a+b) или P = a + a + b + b.
Резюмируем! Для того чтобы вычислить периметр прямоугольника необходимо сложить все его стороны.
Типовые математические и практические задачи:
Исходные данные: Определить периметр прямоугольника с длинами сторон 5 см и 10 см.
Согласно формуле периметр прямоугольника равен = 2 * (5 + 10) = 30 см.
Исходные данные: Определить стороны прямоугольника выраженные целыми числами, если периметр прямоугольника равен 10.
По формуле определяем сумму длин сторон (a + b) = P / 2 = 10 / 2 = 5 Целыми значениями сторон могут быть только значения 1 + 4 = 5 и 2 + 3 = 5
Ответ: Длины сторон могут быть только 2 и 3 или 1 и 4.
Задача №3 (практическая):
Исходные данные: Определить число плинтусов в достаточном количестве для ремонта пола в комнате длиной 5 метров и шириной 3 метра, если длина одного плинтуса равна 3 метра.
Периметр комнаты = 2 * (5 + 3 ) = 16 метров Количество плинтусов = 16 / 3 = 5,33 штук Обычно в строительных магазинах плинтусы продаются не погонными метрами, а поштучно. Поэтому принимаем следующее целое число. Это шесть.
Ответ: Количество плинтусов 6 штук.
В заключение:
Решение задачи вычисления периметра является достаточно простой математической задачей, но имеющей очень важное практическое значение например в строительстве или генеральном планировании территории. На этой странице представлен самый простой онлайн калькулятор для расчета периметра прямоугольника. С помощью этой программы вы в один клик сможете найти периметр прямоугольника, если известны его длина и ширина
С помощью этой программы вы в один клик сможете найти периметр прямоугольника, если известны его длина и ширина
На этой странице представлен самый простой онлайн калькулятор для расчета периметра прямоугольника. С помощью этой программы вы в один клик сможете найти периметр прямоугольника, если известны его длина и ширина.
А о какой фигуре идет речь? Наверное, прямоугольник? Тогда надо перебрать все варианты. Ответов много. Если квадрат, то все проще. Из этого числа извлекаем квадратный корень. И это будет и ширина и длинна одновременно.
Если прямоугольник, то смотрим, на какие множители раскладывается это число ( площадь). И все они могут быть ответом. А с дробными числами их и вовсе огромное количество. Мало начальных данных для получения однозначного ответа.
- Спасибо
- Не нравится
Если речь идет о квадрате, то очень просто и однозначно. Нужно извлечь квадратный корень из площади, получим длину квадрата. У квадрата все стороны равны. В прямоугольнике длина далеко не всегда равна ширине. Если равна, то это уже частный случай — квадрат.
Рассмотрим случай, когда длина прямоугольника не равна ширине. Тогда узнать конкретную длину и ширину, зная только площадь, нельзя, т.к. вариантов будет много. Но если знать еще и соотношение сторон прямоугольника, то вычисление однозначного ответа становится возможным.
Например, есть прямоугольник площадью 100 квадратных единиц, а соотношение сторон неизвестно. Значит, стороны могут быть равными 1 и 100 единиц, 2 и 50, и и 25 и так далее. И никто не отменят варианты с дробными длинами.
Когда соотношение сторон дано, то можно точно вычислить и сами стороны.
Например, площадь прямоугольника равна 100 квадратных единиц, соотношение сторон 1:4.
Тогда по формуле площади можно составить уравнение и найти стороны.
x = 5. Второй корень уравнения — минус 5 — не подходит, т.к. длина не может быть отрицательной.
одна из сторон равна 1х — соответственно, равна 5,
а вторая сторона — 4х = 4*5 = 20 единиц.
Стало быть, стороны этого прямоугольника равны 5 и 20 единицам.
Главная » Учёба и наука » Математика » Найти площадь прямоугольника через стороны
Как вывести диагональ опалубки?
Для упрощения постройки правильной опалубки я делал длину стенок абсолютно равной. Поэтому перекос может получиться только в виде ромба. На рисунке умышлено увеличена степень перекоса опалубки для наглядности. Для исправления ситуации поступили так:
Такое комбинированное перемещение одной из сторон опалубки (северной на рисунке) не было слишком трудном, поскольку колья и первоначальное расположение опалубки соответствовали правильному положению. Поэтому смещение диагонали было минимальным и усилия по «корректировке» положения щитов не вызывали механического напряжения и усилий.
Способ установки углов по равным диагоналям можно использовать только при условии равенства сторон. Равенства диагоналей
будет достаточно!
Для сторон опалубки с большим размером возможно применить правило «золотого» треугольника. Если такой треугольник, согласно теореме Пифагора, имеет стороны 3, 4, то гипотенуза равна 5 единицам. Таким образом, достаточно отмерить на сторонах опалубки части кратные 3 и 4 у вершины прямого угла и тогда расстояние между контрольными точками будет 5 частей! Это и будет гарантией прямых углов и равенства диагоналей!
Для осуществления правильного планирования монтажа опалубки
очень рекомендую использовать метод обноски, который позволяет в любое время монтажных работ производить сверку углов, снимать и повторно устанавливать шнуры периметра фундамента.
Перед заливкой фундамента не поленитесь еще раз проверить диагонали. Это лишним не будет! Бетон невозможно легко и быстро поправить. Ошибки исправлять очень дорого и долго. Фундамент для сруба имеет больше требований к качеству чем фундамент для каменного дома. Раствором уже ничего не выровнять!
Не забудьте перед заливкой для ее легкого демонтажа!
Как это ни странно, но абсолютно все экраны, начиная с дисплеев мониторов, смартфонов и телевизоров, принято считать в дюймах. Причем, при оценке размера видимой рабочей области, указывается именно диагональ, а не ширина и высота. Мы расскажем, почему так принято и что нужно учесть при измерении диагонали экрана телевизора.
Современные телевизоры становятся больше в размерах и тоньше – уже появились модели с диагональю 65 дюймов и толщиной всего 6 мм. Их даже можно вешать на стенку в качестве живых обоев. Поменялось и предназначение самого устройства – теперь это не просто окно в мир телеэфира, но и целый медиацентр с фантастическим качеством изображения, превосходящий по цветовой насыщенности и разрешению картинку и звуковые эффекты в настоящем кинотеатре.

Xiaomi Mi TV 4 с диагональю экрана 65 дюймов и толщиной около 8 мм
Чтобы понять, есть ли в вашей квартире возможность установить ТВ-приемник определенного размера, нужно знать, как измеряется диагональ телевизора. Если вы намерены узнать, какой телевизор у вас был, чтобы купить аппарат существенно большего или наоборот, не намного больше в габаритах, но более современный, есть два способа узнать его размеры.
Кроме того, если вы приобретаете у кого-то телевизор с рук, было бы неплохо узнать точный размер диагонали, т.к. в этом деле каждый дюйм на счету.
Первый способ – взглянуть на тыльную сторону телевизора и найти название и индекс модели. Если у вас нет возможности сделать это, например, аппарат закреплен на стене, то можно поискать инструкцию к телеприемнику, на которой прямо на обложке будет указан индекс. Именно в нем первыми цифрами указана диагональ экрана, например, Samsung UE43NU7100U – 43 дюйма.
Вы можете измерить размер дисплея и более традиционными методами, а именно с помощью рулетки, линейки или простого листа бумаги. Но тогда вам придется выполнить кое-какие вычисления, а значит понадобиться и ручка.

Как это ни дико звучит, но современные телевизоры стали настолько огромными, что метровой (портняжной) линейки может не хватить для измерения диагонали. Поэтому лучше сразу позаботиться о 3 или 5 метровой рулетке. Если под рукой не оказалось этого распространенного инструмента, можно использовать и нитку, которую затем можно измерить чертежной линейкой. Но нитка может тянуться, так, что в этом случае погрешности в полдюйма не избежать.
Необходимые инструменты для работы
Инструменты для разметки фундамента Во время рытья траншей экскаватором убирают шнуры, которые натянуты с выносом от углов, а места сторон отмечают на грунте посыпкой контрастным веществом, например, светлым песком или мелом. Элементы обноски красят яркой краской, чтобы экскаваторщик мог их увидеть и не наехать на разметочные части. После рытья траншеи шнуры натягивают на старое место и проверяют расположение ям или котлованов.
Расчет диагонали фундамента ведется с применением инструментов и приспособлений:
- колья из древесины или ровной арматуры, без кривизны;
- ровные куски металлического профиля или сухой рейки по 2 – 2,5 метра для горизонтального переноса точек;
- капроновый шнур или крепкий шпагат;
- гвозди, шурупы или саморезы;
- угольник, рулетка, молоток, ножницы;
- отвес, водяной или лазерный уровень.
Геодезисты используют теодолит, чтобы размечать углы и давать отметки по высоте. У частников нет такого инструмента, для работы с ним требуется навык. Правильно измерить диагональ дома можно с помощью простых приспособлений.
На угольник закрепляют лазерные указки и строительный уровень — такое приспособление покажет высокую точность при разметке. Продаются транспортиры и угольники большого размера, лучше взять такие, чтобы было удобнее переносить линии плана на местность. Первоначальная разметка очень важна для начала строительства, поэтому желательно высчитать диагональ несколько раз, чтобы быть уверенным в правильности работы.
Способы измерения диагонали телевизора
Вообще, всего два способа узнать диагональ телевизора. Самый правильный – открыть технический паспорт. На одной из страниц должна находиться эта информация, к тому же многие производители указывают размер на заводской коробке TV.
Также найти эту информацию легко в интернете, достаточно вбить в поисковую строку модель устройства. Не редко производитель указывает данное расстояние на корпусе. Но нужно быть сконцентрированным, так как в такой ситуации число может быть как в сантиметрах, так и в дюймах.
Но бывают разные ситуации, когда необходимо самостоятельно померить диагональ телевизора. В таком варианте событий понадобится рулетка, можно воспользоваться линейкой, но в таком случае будут большие погрешности. Для измерения достаточно узнать дистанцию от левого нижнего угла до верхнего правого. Если необходимо посчитать измерения в дюймах, то полученное число следует поделить на 2.54.
Некоторые телевизоры обладают выпуклым экраном. Из-за этого измерение диагонали телевизора рулеткой превращается в кошмар наяву. Чтобы избежать мучений, следует приготовить обычную длинную нитку. Один конец нужно приложить к левому нижнему углу, после чего протянуть к верхнему правому. Зафиксировать пальцем место «соединения» нитки и верхнего угла, затем замерить длину. Получившееся число и есть диагональ, только в сантиметрах.
Свойства и линии
Из-за того, что прямоугольник — это параллелограмм, все свойства последнего справедливы и к нему. В первую очередь для него характерно, что противоположные стороны являются параллельными, то есть лежат на непересекающихся прямых. Отсюда следует, что фигуры отличаются друг от друга только размерами двух граней.
К основным свойствам прямоугольника относят:
- противолежащие стороны имеют равную длину: AB = CD, BC = AD;
- все углы равны 90 градусов;
- отрезки, обозначающие ширину и длину, всегда перпендикулярные друг другу: AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB;
- сумма любых двух углов фигуры равняется 180 градусов, соответственно всех четырёх — 360;
- в четырёхугольном теле можно провести 2 диагонали, длины которых будут совпадать по величине: AB = BC;
- сумма квадратов диагональных отрезков равняется удвоенной сумме квадратов сторон фигуры: AC2 + BD2 = 2 (AB2 + BC2);
- построенная диагональ разделяет прямоугольник на 2 одинаковые фигуры — прямоугольные треугольники;
- точка пересечения прямых линий, соединяющая попарно противоположные углы, является центром фигуры и описанной окружности;
- диагонали в месте пересечения разделяются на 4 равных отрезка;
- в многоугольник, у которого длина не равна ширине, вписать окружность нельзя, поэтому её можно построить только для частных случаев прямоугольника.

На свойстве, что сложенные квадраты диагоналей можно найти как сумму квадратов всех его сторон, построено решение многих геометрических задач. Нелишним будет доказательство теоремы. Пусть имеется прямоугольник, у которого линии AC и BD — диагонали. Если изобразить многоугольник на рисунке и построить отрезки, можно увидеть, что каждая диагональ делит фигуру на 2 треугольника: ABC и BDC.
Используя теорему косинусов, можно записать: AC2 = AB2 + BC2 — 2 * AB * BC * cos (ABC); BD2 = CD2 + BC2 — 2 * CD * BC * cos (BCD). После сложения полученных выражений получится запись: AC2 + BD2 = AB2 + BC2 — 2 * AB * BC * cos (ABC) + CD2 + BC2 — 2 * CD * BC * cos (BCD).
Так как по свойству прямоугольной фигуры противоположные стороны равны, уравнение примет вид: AC2 + BD2 = 2AB2 + 2BC2 — 2 * AB * BC * cos (ABC) — 2 * AB * BC * cos (BCD). Учитывая, что сумма двух углов равняется 180, полученное выражение можно переписать так: AC2 + BD 2 = 2 (AB 2 + BC 2). Что и следовало доказать.
Контроль за собой: как вывести диагональ фундамента
Способ первый
Самый первый вариант известен со времен античности. Имеем линию стены и точку – будущий угол дома. От этой точки и откладываем перпендикуляр. Для чего вспоминаем школьный курс геометрии: a2+b2=c2. Где a и b являются катетами, а c – гипотенуза. Чтобы не мучиться с дробями и квадратными корнями, берем простые числа, позволяющие обойтись без дробей: 3, 4 и 5. Первый, второй катет и гипотенуза соответственно
При этом неважно, какие единицы измерения выбраны: метры, футы, локти. Главное, чтобы размеры сторон треугольника были кратны 3 4 и 5. Можно сделать отдельный треугольник с таким соотношением сторон, или отложить эти размеры на шнурах, обозначающие границы будущего фундамента (от точки пересечения их – от угла) – это катеты
А потом разворачивать вторую стену, пока расстояние между внешними точками не окажется равно гипотенузе. Это и будет прямоугольный треугольник. Далее продолжаем второй катет до нужных размеров (длина будущей стены), а затем повторяем операцию дважды – четвертый угол получится сам
Можно сделать отдельный треугольник с таким соотношением сторон, или отложить эти размеры на шнурах, обозначающие границы будущего фундамента (от точки пересечения их – от угла) – это катеты. А потом разворачивать вторую стену, пока расстояние между внешними точками не окажется равно гипотенузе. Это и будет прямоугольный треугольник. Далее продолжаем второй катет до нужных размеров (длина будущей стены), а затем повторяем операцию дважды – четвертый угол получится сам.
Способ второй
Несколько проще способ с дугами, хотя он требует определенного оперативного простора.
Есть отрезок – будущая стена. Продолжаем эту прямую дальше на такое же расстояние. Получаем линию, центр которой – это будущий угол фундамента. Затем от крайних точек (равноудаленных от центра-угла на расстояние, равное длине стены) рисуют две дуги – их радиус может быть произвольный, только бы он был больше длины стены. То есть берут веревку, один конец который петлей крепят за столбик, отмечающий край этого удвоенного отрезка, а ко второму концу привязывают палку – она сыграет роль стилоса, черты. И на грунте рисуют этой палкой дугу. Ограничителем служит веревка, шнур.
Процедуру повторяют от второй крайней точки. Соответственно, две дуги эти пересекаются. От точки пересечения дуг проводят прямую к середине нашего удвоенного отрезка – углу будущего фундамента. Так получают искомый перпендикуляр.
И еще нужно отметить, что способ с дугами хорошо работает на небольших фундаментах: под баню или под гараж. Более масштабные разметки под дом лучше проводить или с помощью треугольника, или третьим методом.
Третий способ
Тут потребуется калькулятор. Сначала связывают шнур в петлю – длина петли равна периметру искомого прямоугольника. Потом на петле отмечают точки углов – то есть откладывают отрезки, равные длине каждой стены. Понятно, что делать это следует последовательно. Затем на калькуляторе как можно точнее считают длину диагонали – это гипотенуза, а катетами в расчетах выступают стены – их длина. Затем отмеряют два куска шнура, чья длина чуть больше гипотенузы – запас нужен для вязания узлов.
Делают отметки на этих двух шнурах (запас на вязки оставляют с обеих сторон. Затем шнуры эти привязывают к петле-периметру. Так, чтобы они шли из одного угла в другой по диагонали. То есть через угол.
Затем растягивают полученный «конверт» на месте будущего дома. Как только все шнуры одинаково натянуты (не должно быть провисаний ни снаружи, ни внутри этой паутины), то это и будет правильный прямоугольник.
Делаем разметку под фундамент правильно
Необходимые инструменты
Чтобы разметка под фундамент была точной и быстрой в выполнении необходимо запастись следующими приборами и материалами:
Инструменты для разметки фундамента
- рулетка с большой длиной измерительной ленты (в идеале равной или больше длины самой протяженной стены дома);
- деревянные колышки или арматурные стержни (выбор зависит от имеющихся материалов и плотности грунта основания);
- строительный угольник (имеет углы с величинами 30,60 и 90 градусов);
- прочный шнур;
- деревянные рейки;
- зажимы, прищепки или гвозди для закрепления шнура к колышкам;
- строительный уровень (можно приобрести недорогой пузырьковый, лазерный существенно облегчит работу, но имеет высокую стоимость).
Если есть возможность, можно также использовать нивелир, но его покупка для строительства одного здания нецелесообразна. Также при себе нужно иметь ножницы для нарезки шнура, молоток для забивки гвоздей, калькулятор для проведения необходимых расчетов.
Необходимость расчета диагонали фундамента
При неверном расчете диагонали все дальнейшее строительство будет расходиться с планом Проект предполагает подбор конструктивных элементов точно в размер, чтобы при строительстве не возникало перекосов. Длина балки или плиты перекрытия берется с требуемой глубиной опирания, которая принимается по конструктивному расчету. Во время разметки фундамента нужна предельная точность, т.к. отклонение в размерах повлечет расхождение вертикальных конструкций.
Горизонтальные элементы могут не влезть в проектное положение или вываливаться из монтажного пространства, поэтому потребуется перерасчет длины, а также других показателей.
Правильная разметка основания ведет к приятным бонусам при возведении здания:
- простота строительства стен и применения сборных элементов;
- соблюдение предусмотренной проектом экономии средств и материалов;
- сооружение объекта без отклонений от проекта.
Перед тем как вымерить диагональ фундамента, нужно выровнять строительную площадку, чтобы удобно было размечать линии на местности. Почти всегда строительные конструкции и материалы от утеплительных матов до досок и стеновых щитов имеют прямые углы, поэтому фундамент также размечают с учетом этих требований.
Сложности при неправильной разметке

Нарушение геометрии фундамента снижает прочность стен Неправильная переноска размеров на местность и пренебрежение сравнением диагоналей приведет к тому, что на поверхности земли появится ромб или трапеция. При устройстве самого фундамента это может и не станет заметно, но первая укладка плит над подвалом выявит несоответствия и приведет к потерям времени для перерасчета сборных элементов или переделке основания.
Если плита опирается меньше требуемой глубины, после получения нагрузки от оборудования или людей она может обломить опорную часть стены и упасть. Такая неприятность коснется горизонтальных элементов перекрытия на всех этажах высотного строения и будет повторяться вплоть до кровли.
Выполнить устройство крыши трудно, если не соответствуют размеры между балками, фермы приходится ставить большего размера, а в других местах уменьшать габариты. Увеличивается трудоемкость работ, т.к. исполнитель выступает в несвойственной для него роли конструктора и проектировщика.
Усложнится установка кровельного покрытия, т.к. листы профнастила или шифера выпускаются с прямыми углами. Сборные угловые элементы водоотлива также рассчитаны на установку под 90°, желоб будет отходить от края кровли, а вода попадет на вертикальные ограждения, стены будут отсыревать.
Инструкция по разметке прямоугольного фундамента
Способ 1. Правила золотого треугольника (т.Пифагора)
Рассмотрим на примере построение прямоугольного фундамента с размерами 6х8м с помощью золотого треугольника (т.Пифагора).
1. Размечаем первую сторону фундамента. Это самая простая часть в построении нашего прямоугольника. Главное, что нужно помнить. Если хотим чтобы наш фундамент (дом) был параллелен одной из сторон забора либо другого объекта на участке или за его пределами, то первую линию нашего фундамента делаем равноудаленной от выбранного нами объекта. Данную процедуру мы описывали выше. Для размещения первой бечевки можно использовать колушки, прочно закрепленные в грунте, но в идеальном варианте для данной цели использовать обноску. Ее и будем использовать. Расстояние между обносками для данной стороны сделаем 14м: между обносками и будущими углами по 3м и 8м под фундамент.
2. Натягиваем вторую бечевку максимально перпендикулярно первой. Идеально перпендикулярно на практике натянуть сложно, поэтому на рисунке мы также отобразили ее не много отклоненной.
3. Скрепляем обе бечевки в точке пересечения. Скрепить можно скобкой либо скотчем. Главное чтобы надежно.
4. Приступаем к формированию прямого угла с применением теоремы Пифагора. Будем строить прямоугольный треугольник с катетами 3 на 4 метра и гипотенузой 5 метров. Для начала отмеряем на первой бечевке 4 метра от места пересечения бечевок, а на второй 3 метра. Ставим отметки на шнурке с помощью скотча (прищепка и т.п.).
5. Соединяем рулеткой обе отметки. Один конец рулетки фиксируем у отметки в 4 метра и ведем в сторону отметки в 3 метра на другой бечевке.
6. Если у нас прямоугольный треугольник, то обе отметки должны сойтись при расстоянии в 5 метров. В нашем случае отметки не сошлись. Поэтому перемещаем бечевку в нашем случае вправо до того момента когда отметка на 3 м совпадет с делением рулетки на 5 м.
7. В итоге у нас получился прямоугольный треугольник с углом в 90⁰ между двумя бечевками.
8. Больше отметки нам не нужны и их можно убрать.
9. Приступаем к построению прямоугольника. Отмеряем на обеих бечевках длины сторон нашего фундамента 6 и 8 метров соответственно. Ставим отметки на бечевках.
10. Натягиваем третью бечевку максимально перпендикулярно к первой бечевке. Скрепляем обе бечевки на отметке в 8 м.
11. Натягиваем четвертую бечевку максимально перпендикулярно ко второй бечевке. Скрепляем обе бечевки на отметки в 6 метров.
12. Делаем отметки на третьей бечевке 6 метров и на четвертой 8 метров.
13. Чтобы получить четырехугольник с прямыми углами в нашем случае необходимо, чтобы обе отметки на третьей и четвертой бечевках совпали. Для этого перемещаем обе бечевки до момента соединения отметок.
14. В итоге, если все правильно измерили, то у нас должен получиться правильный прямоугольник. Давайте проверим, получился ли он с помощью измерения диагоналей.
15. Измеряем длины диагоналей. Если они одинаковые, как в нашем случае, мы имеем правильный прямоугольник. Диагонали имеют одинаковую длину и в равнобедренной трапеции. Но у нас известен один угол в 90⁰, а в равнобедренной трапеции таких углов нет.
16. Готовая разметка прямоугольного фундамента с применением теоремы Пифагора. www.gvozdem.ru
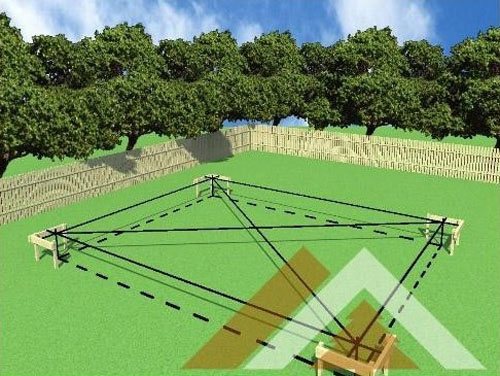
Способ 2. Паутина
Очень простой способ сделать разметку в виде прямоугольника с углами в 90⁰. Самое главное что нам понадобится — это бечевка, которая не растягивается, и точность ваших измерений с помощью рулетки.
1. Нарезаем куски бечевки, которые нам понадобятся для формирования разметки. В данном примере мы строим фундамент со сторонами 6 на 8 метров. Также для правильного построения прямоугольника нам понадобятся равные диагонали, которые для прямоугольника 6 на 8 метров будут равны 10 метрам (т.Пифагора описана выше). Также нужно взять запас длины бечевок на крепление.
2. Соединяем нашу «паутину» как на рисунке. Скрепляем стороны с диагоналями в 4 местах по углам. Сами диагонали в точке пересечения скреплять не нужно.
3. Натягиваем первую бечевку (точки 1,2). Крепить ее будем с помощью колышков. Главное чтобы колышки крепко держались в земле и при натяжении нашей конструкции их не увело. Этот важный момент нужно учесть.
4. Натягиваем угол 3. Главное условие чтобы бечевка 1-3 и диагональ 2-3 не провисали и были максимально натянуты. После фиксации с помощь колышка в точке 3 мы имеем угол в точке 1 в 90⁰.
5. Натягиваем угол 4 и устанавливаем колышек. Следим, чтобы бечевка в точках 2-4, 3-4 и диагональ 1-4 не провисали и были максимально натянуты.
6. Если соблюдены все условия, то в результате у нас должен получиться прямоугольник с углами максимально близкими 90⁰.
Советы
- Размечая расположение траншей под столбчатое основание-фундамент удобнее пользоваться двухъярусной обноской. Ее нижний ярус — высота столбовых опор, верхний — ростверка.
- Под ленточный натягивают по две параллельные веревки-ориентир для каждой стороны. Расстояние между ними равно ширине заливаемой ленты. Высота натяжения — верхний уровень ленты-основания. Если планируется рытье траншей трактором, веревочные ориентиры опускаются вниз (до грунта). Вдоль них (с внешней и внутренней стороны) копаются неглубокие канавки.
- Под плитный — шнуры располагают на уровне верхней плоскости плиты (верхний ярус обноски).
- Шнуры-ориентиры должны быть крепко натянуты. Их убирают после окончания рытья траншеи.